一致,在三角形ABC中,AC 2根号六
来源:学生作业帮助网 编辑:作业帮 时间:2024/11/10 14:44:08
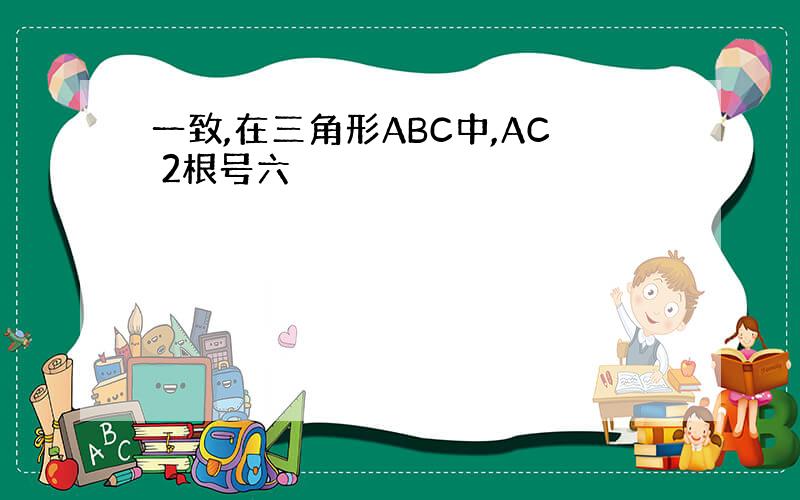
A=45`a/sinA=c/sinCc=6*根号2
(1)△ABC是直角三角形;(2)延长CD至E,使得CD=DE,∵AB与CE互相平分,∴四边形AEBC是平行四边形∵4CD2=CE2,所以AC2+BC2=CE2,所以∠CAE为直角,又∵四边形AEBC
∵△ABC为直角三角形,AB为斜边,∴AC2+BC2=AB2,又AB=2,∴AC2+BC2=AB2=4,则AB2+BC2+CA2=AB2+(BC2+CA2)=4+4=8.故答案为:8
AC2-CD2=AD2=>AC2=CD2+AD2……1=>角ADC=90=>角ADB=90=>AB2=AD2+BD2=……2=>1,2两式相减AB2-AC2=AD3+BD2-CD2-AD2=BD2-C
解题思路:根据直角三角形的知识可求解题过程:最终答案:略
线段BD、CE、DE之间存在的数量关系为DE=BD+CE,理由为:由BF、CF分别为角平分线,利用角平分线定义得到两对角相等,再由DE与BC平行,得到两对内错角相等,等量代换及等角对等边得到BD=DF
(1)证明:∵AC2=AD•AB,∠A=∠A,∴△ACD∽△ABC,∴∠ACD=∠B=36°,∵AC=BC,∴∠A=∠ACD=∠B=36°,∴三角形ADC是等腰三角形,∵∠BDC=∠A+∠ACD=72
只需条件:角A等于36度,AC=BC,若AB=.1,即可求出AC,其他条件是多余的.作CE⊥AB于E,∵AC=BC,∴AE=½AB=0.05AB=AE/cosA=0.05/cos36&o
∵DE为BC的垂直平分线,∴CE=BE,∴BE2-AE2=CE2-AE2=AC2,即BE2=AC2+AE2.
已知,CM是Rt△ABC斜边上的中线,(题中应该是∠A小于∠B)可得:CM=AM,所以,∠ACM=∠BAC.∠BCD=90°-∠B=∠BAC=∠ACM=∠DCM.因为,∠BCD+∠ACM+∠DCM=9
你确定你的条件都写了吗,我咋感觉少个条件
a+b=4ab=2a^2+b^2=(a+b)^2-2ab=12=斜边的平方RT三角形ABC的外接圆的半径就是斜边的一半所以为根号3
已知,AD=AC,BE=BC,可得:∠ADC=∠ACD,∠BEC=∠BCE,即有:∠EDC=∠ACD=∠ACE+∠ECD,∠DEC=∠BCE=∠BCD+∠ECD,∠ECD=180°-(∠EDC+∠DE
因为BD=CDBE^2+ED^2=BD^2所以CD^2=BD^2=BE^2+ED^2所以AD^2=AC^2+CD^2=AC^2+BD^2=AC^2+BE^2+ED^2又因为DE垂直于AB所以AD^2=
作高线AE,很易证再问:那是几何方法,我认为可以用直线方程的思想来证明这道题,但是不太容易,所以想找一种更为简单的方法再答:那就用余弦定理从cosADC=-cosADB表示出来,相加就行了
∵AC2+AB2=BC2,∴△ABC是直角三角形,∴∠A=90°,∴∠B+∠C=180°-90°=90°,故答案为:90°.
解题思路:根据题意,由正弦定理和余弦定理可求解题过程:见附件最终答案:略
∵AD⊥BC于D,∴∠ADB=∠ADC=90°∵AB=3,BD=2∴AD2=AB2-BD2=5∵DC=1,∴AC2=AD2+DC2=5+1=6.
∵AE是高,∴△ABE和△ACE是直角三角形,∴AB2=BE2+AE2,AC2=AE2+EC2,∴AB2-AC2=BE2-EC2=(BE+CE)(BE-CE)=BC(BD+DE-CE),∵AD是中线,