不定积分x (1-2x^2)^1 2dx-搜答案-大师作文网

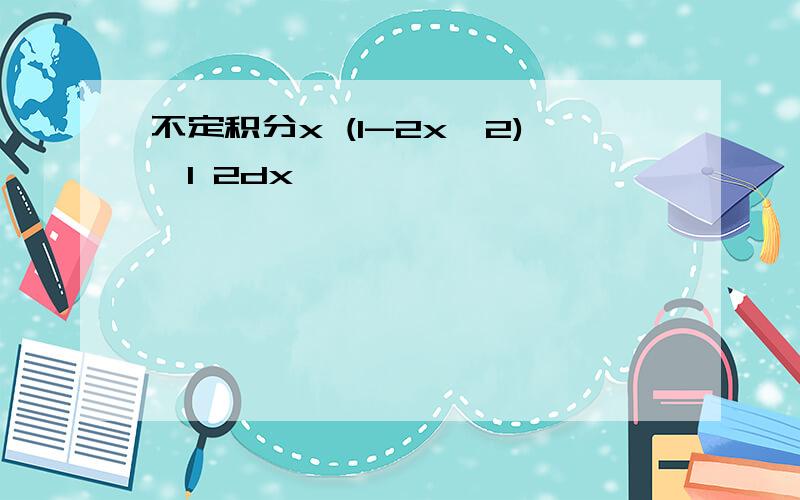
表达式不够明确,可能被理解为两种情形：x^2(√x)/(1-x)或(x^2)*√[x/(1-x)]；如是第一种情形积分：设t=√x,则dx=2tdt；∫[x^2(√x)/(1-x)]dx=∫[2t^6

∫[2x/(x^2+x+1)]dx=∫[(2x+1)/(x^2+x+1)]dx-∫dx/(x^2+x+1)=ln|x^2+x+1|-∫dx/(x^2+x+1)considerx^2+x+1=(x+1/

∫(X^2+X+1/X)dx=x^3/3+x^2/2+lnx+C

原式=∫x*(csc^2x+1)=∫x*csc^2x+x（分开积分）前面=-x*cotx+∫cotx=-x*cotx+ln|sinx|后面=1/2x^2记得加C

∫(x^2-1)sin2xdx先括号拆开=∫x^2*sin2xdx-∫sin2xdx=-1/2*∫x^2dcos2x-1/2*∫sin2xd2x先凑微分=-1/2*∫x^2dcos2x-1/2*∫si

原式=∫(x+1)/x²+∫xlnxdx=∫x/x²+∫1/x²+1/2∫lnxdx²=∫1/x+∫1/x²+1/2*x²lnx-1/2∫x

1/(x+1)(x+2)(x+3)=1/(x+1)[1/(x+2)-1/(x+3)]=1/[(x+1)(x+2)]-1/[(x+1)(x+3)]=1/(x+1)-1/(x+2)-1/2[1/(x+1)

∫x^7dx/(x^4+2)=(1/4)∫x^4d(x^4)/(x^4+2)=(1/4)x^4-(1/4)ln(x^4+2)+C∫（3x^4+x^3+4x^2+1)dx/(x^5+2x^3+x)=∫(

不定积分(x+1)^3/x^2

首先展开,再拆项得：X+3+3/X+1/X^2依次积分有：0.5X^2+3X+3ln|X|-1/X

∫x^3/√(1-x^2)dxletx=sinydx=cosydy∫x^3/√(1-x^2)dx=∫(siny)^3dy=-∫(siny)^2dcosy=-∫[1-(cosy)^2]dcosy=(co

再答：

分部积分法∫xe^x/(1+x)^2dx＝－∫xe^xd[1/(1+x)]＝－xe^x/(1+x)＋∫(1+x)e^x×1/(1+x)dx＝－xe^x/(1+x)＋∫e^xdx＝－xe^x/(1+x)

1/(1+x^2)d(1+x^2)=ln(1+x^2)+C

采用分部积分了!因为∫[dx/(lnx-x)+(1-x)dx/(x-lnx)^2]=∫dx/(lnx-x)+∫x(1/x-1)dx/(x-lnx)^2=∫dx/(lnx-x)+∫xd(lnx-x)/(

∫［（x－1）/（x^2＋3）］dx＝∫［x/（x^2＋3）］dx－∫［1/（x^2＋3）］dx＝（1/2）∫［1/（x^2＋3）］d（x^2＋3）－（1/√3）∫｛1/［（x/√3）^2＋1］｝d（

答：1.原式=∫1/[(x+1)^2+4]dx=1/4∫1/[((x+1)/2)^2+1]dx=1/2*arctan[(x+1)/2]+C2.原式=1/2∫1/x-x^6/(x^7+2)dx=1/2[