- lambertw(0, -exp(- x^2 C3 - 1)) - 1
来源:学生作业帮助网 编辑:作业帮 时间:2024/11/12 18:49:34
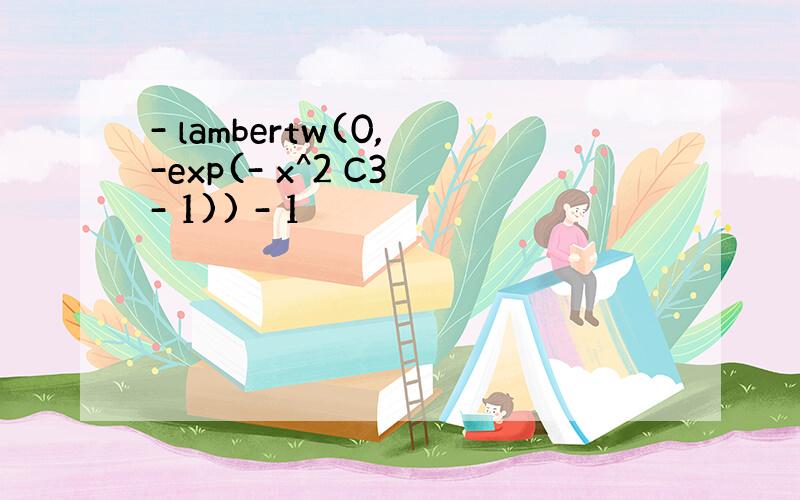
今夜,月朗,星稀.篱边黄花幽香,窗外竹林清响,月斜柳梢,灯映兰房,寒彻一番西风,淡泊一杯愁绪.人不寐,已三更,披一袭青衫,掩了门扉,信步闲庭.守在回忆的路口,等你姗姗而来.从未搁浅的期待,如今夜的坠叶
lambertw是matlab的一个函数意思是x*e^x=W;x=lambertw(W)其实你只要将这个结果再次放入Command窗口就可以运行处结果了例如:>>-lambertw(0,-5/22)a
limx趋近于0【ex-x】(1/x^2)=limx趋近于0【e^x-x】^(1/x^2)取对数:原式=1/x²ln(e^x-x)=【ln(e^x-x)】/x²罗比达法则:上下求导
ln[x]>[1/(e^x)-(2/ex)]记f(x)=ln[x]-e^(-x)+(2/ex),等价证明:当x>0时,f(x)>0.由一阶导数f’(x)=1/x+1/e^x-2/ex^2=0得:1/x
用罗比达法则:上下求导,f(x)=e^x,代人X=0,就=1
【解法1】利用函数的单调性进行证明.令f(x)=ex-(1+x),则f′(x)=ex-1.令f′(x)=0,求得x=0.当x∈(-∞,0)时,f′(x)<0,故f(x)在(-∞,0]上严格单调减少;当
这个命题是错误的.只有当x>0时才成立.令f(x)=e^x-1-xf'(x)=e^x-1>0(当x>0时)故f(x)在(0,+∞)上单增.f(0)=0因此在(0,+∞)上恒有e^x>1+x
(2.6+3-e)X=-6X=-6/(2.6+3-e)如果还要精确计算的话e=2.7128……代入即可得到答案
证明:令f(x)=ex−1−x−12x2,则f'(x)=ex-1-x,再令g(x)=f'(x),则g'(x)=ex-1,∵x>0,∴ex-1>0,即g'(x)>0,∴g(x)在[0,+∞)上为增函数,
x=-2^(1/2)-lambertw(0,-log(2)/2^(2^(1/2)))/log(2)x=-0.8653再问:nihao,怎么转化的啊?再答:将-2^(1/2)-lambertw(0,-l
是超越函数超越方程的解
lambertw是一个函数,lambertw(x)表示方程w*exp(w)=x的解w.求解超越方程x2^x=1的解.>>solve('x*2^x-1')%求解超越方程ans=1/log(2)*lamb
ex前...如exwife前妻
deusexmachinaph.【拉】1.(小说戏剧情节中牵强扯入的)解围人物(或事件)2.意外介入而扭转局面的人
因为f(x)是R上的偶函数所以f(-x)=e^-x/a+a/e^-x=1/ae^x+ae^x=f(x)即e^x/a+a/e^x=1/ae^x+ae^x整理得1/a(e^x+1/e^x)=a(e^x+1
国际贸易术语E组Ex交货EXworks(EXW)卖方仓库交货/工厂交货
f(x)=(ex-1)/(ex+1)=(e^x+1-2)/(e^x+1)=1-2/(e^x+1)设x2>x1>0,则f(x2)-f(x1)=[1-2/(e^x2+1)]-[1-2/(e^x
令y=e^x-ex则求导得到y'=e^x-e令y'=0得到x=1所以在(0,1)是减区间在(1,+∞)是增区间y的最小值是x=1时也就是ymin=e^1-e=0所以y始终>0也就是e^x>ex