在RT三角形ABC中,AD为高,BE是角平分线,求证BE`AB=BF`BC
来源:学生作业帮助网 编辑:作业帮 时间:2024/11/10 23:24:35
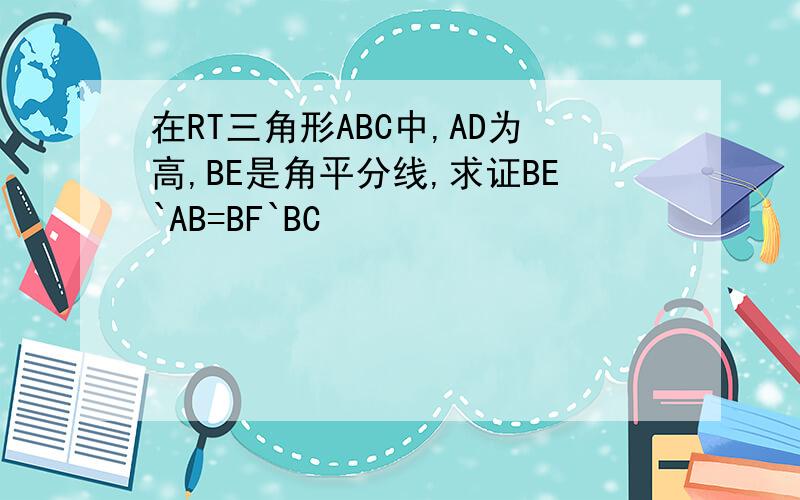
如图,⊿EAB≌⊿EGB(AAS) EG=EA AB=GB ∴⊿FAB≌⊿FGB(SAS).GF=FA∠CAD=90&am
因为AB=AC所以直角三角形的高AD垂直于BC因为BD垂直于DCBD垂直于AD所以BD垂直于面ADC又因BD是品面ABD上的一条直线所以平面ABD垂直平面BDC
如图,在Rt△ABC中,CD是斜边AB上的高,∠ACB=∠CDB=90°,又∵∠A=∠DCB,∴△ACD∽△CBD,则 ADCD=CDBD.则CD2=AD•BD=8×4=32.∴
4tanA=8:2=4
证明:因为AB⊥AC,AD⊥BC,所以AB.AC=0,AD.DB=0,AD.DC=0.又因为AB.AC=(AD+DB).(AD+DC)=AD^2+AD.DC+DB.AD+DB.DC=AD^2+DB.D
证明:∵AC^2=3BC^2,Rt△ABC中,∠ACB=90°∴AC^2+BC^2=AB^2∴3BC^2+BC^2=AB^2∴AB=2BC∴∠A=30°(在直角三角形是,如果一直角边等于斜边的一半,那
易证△ACD∽△BCD(射影定理)CD×CD=AD×BD=2CD=「2两三角形周长之比=边之比=1∶「2=「2∶2
过F做FG垂直于BC交BC与G,三角形ABF与三角形BFG全等,角AFB=角GFB,因为AD平行与FG,则角AEF=角BFG,故角AFB=角AEF,得AEF是等腰三角形
AD是高,用勾股定理有AB^2=BD^2+AD^2,15^2=BD^2+12^2,BD=9AC^2=CD^2+AD^2,13^2=CD^2+12^2,CD=sqrt(13)所以面积=1/2*BC*AD
当点D在线段BC上时是42(此时∠C是锐角)当点D在BC延长线上时是32(此时∠C是钝角)
(1)在三角形ACB与三角形BDA中AC=BD角CAB=角DBAAB=BA所以三角形ACB全等于三角形BDA.(SAS)所以角ABC=角DAB.因为角CAB=角CAD+角DAB角DBA=角DBE+角E
已知,CM是Rt△ABC斜边上的中线,(题中应该是∠A小于∠B)可得:CM=AM,所以,∠ACM=∠BAC.∠BCD=90°-∠B=∠BAC=∠ACM=∠DCM.因为,∠BCD+∠ACM+∠DCM=9
作Q关于AB,AC对称点Q1,Q2∵PQ=PQ1,QR=Q2R∴PQ+QR+PR>=Q1Q2,(当P,R都在A点取等)∵∠Q1AB=∠QAB,∠Q2AC=∠QAC∴∠Q1AB+∠Q2AC=∠QAB+∠
题:在Rt△ABC中,已知AD是斜边BC上的高,S△ABC=12,BC=8.求:以BD、CD的长度为根,作一个关于x的一元二次方程.∵S△ABC=(1/2)AD*BC=12.AD=12*2/BC=24
设ad将直角A分为角1,角2,be将角B分为角3、角4因为ad为bc的高,所以角C+角1=90°又角1+角2=90°所以角2=角C又角afe=角3+角2(三角形abf)角aef=角4+角C(三角形be
连接I1D,I2D,分别平分△ABD和△ACD的直角,则I1D⊥I2D,连接AI1,AI2,△AI1D∽△CI2D,I1D/I2D=AD/DC,Rt△ACD∽Rt△I1I2D,∠I1I2D=∠C,四边
a+b=4ab=2a^2+b^2=(a+b)^2-2ab=12=斜边的平方RT三角形ABC的外接圆的半径就是斜边的一半所以为根号3
因为AD是斜边BC上的高,所以CD垂直于AD.又因为角BDC是直角,即CD垂直于BD且AD与BD相交,所以根据线面垂直判定定理,CD垂直于平面ABD又因为CD在平面BDC内,所以根据面面垂直判定定理,
AC^2=CD^2+AD^2,AB^2=AD^2+DB^2,AC^2+AB^2=2*AD^2+DB^2+CD^2=DB^2+CD^2+2*BD*DC=(CD+DB)^2=BC^2三角形ABC为RT三角