A2-2A-4E
来源:学生作业帮助网 编辑:作业帮 时间:2024/11/13 20:27:57
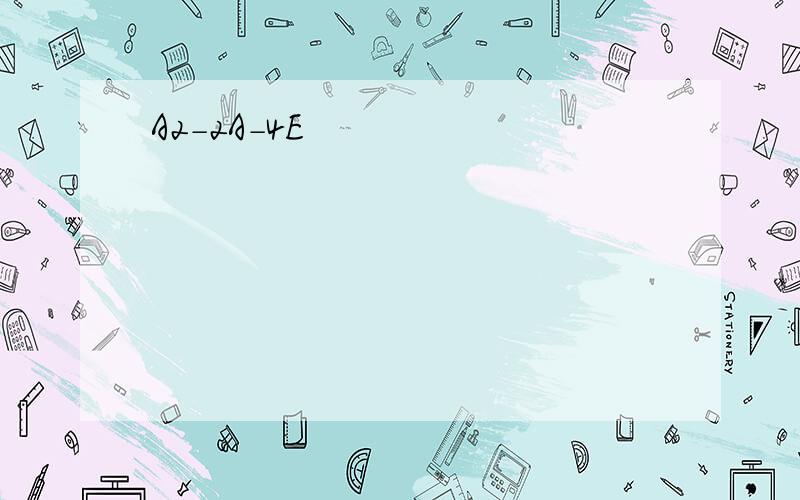
解:因为A^2-2A-E=0所以A(A-2E)=E所以A-2E可逆,且(A-2E)^-1=A.
∵a2(a2-2)-2a2+4=a4-2a2-2a2+4=a4-4a2+4=(a2-2)2≥0,又∵a为有理数,∴a2不等于2,∴整式≠0∴整式a2(a2-2)-2a2+4的值恒为正数.故选B.
∵a2+2a=1,∴2a2+4a-1=2(a2+2a)-1=1.
-√3-2再问:能否写一下过程呢???再答:[(a+1)/(a²-a)+4/(1-a²)]/[(a²+2a-3)/(a²+3a)]=[(a+1)/a(a-1)+
原式=[(a²-4)/(a²-4a+3)]×[(a-3)/(a²+3a+2)]={(a-2)(a+2)/[(a-1)(a-3)]}×{(a-3)/[(a+1)(a+2)]
A的全部特征值为1,2,3,4所以2A^2+3A+E的特征值为5,11,19,29所以|2A^2+3A+E|=30305.注:若λ是A的特征值,则f(λ)是f(A)的特征值.这里f(x)=x^2+3*
利用特征值和特征多项式的关系设矩阵A的特征值x那么利用特征值与矩阵多项式关系可知A2-E的特征值为f(x)=x^2-1即有f(2)=2^2-1=3
∵a2-3a+1=0,∴a2-3a=-1,a+1a=3,1+a2=3a,∴4a2-9a-2+91+a2,=4(a2-3a)+93a+3a-2,=4×(-1)+3(1a+a)-2,=-4+3×3-2,=
根据4+2a的大于0、小于0分别讨论当4+2a>=0,即a>=-2,原式=4+2a/根号a2+1当4+2a
1/(a+1)-(a+3)/(a^2-1)*(a^2-2a+1)/a^2+4a+3)=1/(a+1)-(a+3)/[(a-1)(a+1)]*(a-1)^2/[(a+1)(a+3)]=1/(a+1)-(
原式=(a²+4a+4-6-3a)/(a²+4a+4)×(a²+2a)/(4a-4)=(a+2)(a-1)/(a+2)²×a(a+2)/4(a-1)=a/4
a2-2a=-1,方程两边都乘以-2,得-2a2+4a=-2,方程两边都加3,得3-2a2+4a=3+(-2)=1.
∵a2+2a+1=0,∴2a2+4a-3=2(a2+2a+1)-5=0-5=-5.
要证明E-2A可逆我们可以假设其可逆,并设其逆为aE+bA则(E-2A)(aE+bA)=E那么aE+(b-2a)A-2bA^2=E又A^2=A那么(a-1)E-(b+2a)A=0所以a-1=0,b+2
(a2-1)/(a2+2a+1)除以(a2-a)/(a+1)(a-2/(a+3)除以(a2-4)/(a2+6a+9)=﹙a²-1﹚/﹙a²+2a+1﹚×﹙a+1﹚/﹙a²
A^2-3A+2E=(A-E)(A-2E)=4E, 由逆矩阵的定义有:A-E=1/4(A-2E)
a³-2a²-4a+3=a³-2a²-3a-a+3=a(a²-2a-3)-(a-3)=a(a+1)(a-3)-(a-3)=(a-3)(a²+
a2+b2+2a-4b+5=a2+2a+1b2-4b+4=(a+1)^2+(b-4)^2=0平方和为0,两个都为0a=-1b=4-2a2-a=-1
若存在B使B(A+E)=E,就可以了A2-2A-8E=0--->A2-2A-3E=5E---->(A+E)(A-3E)=5E---->(A+E)(A/5-3/5E)=E所以(A/5-3/5E)此类问题