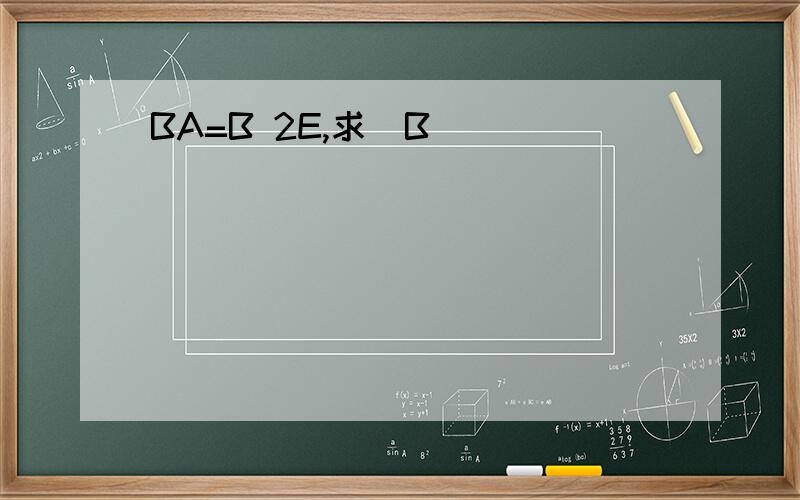
BA=B 2E,求|B|

BC*CA=CA*AB===>CA(BC+BA)=0===>CA⊥(BC+BA)根据向量的平行四边形法则可知:菱形ABCD的对角线BD=BC+BA,CA⊥BD,|BA|=|BC|,设BD,CA的交点为

答案是根号10.过D作DE平行AB,交AC于F点.易知AC垂直DE.那么三角形FEC和三角形FAD都为等腰直角三角形.三角形FDC为直角三角形.计算可知DF=1,FC=3.在直角三角形FDC中,由勾股

原式=a(a−b)+b(a−b)−a2a(a−b)÷a(a+b)−b(a+b)−a2a(a+b)=−b2a(a−b)•a(a+b)−b2=a+ba−b，由3a-2b=0知，3a=2b，则原式=a+ba

/>A^-1BA=4A+2BA两边同时左乘A得BA=4A²+2ABA（E-2A）BA=4A²两边同时右乘A^-1得（E-2A）B=4A那么B=（E-2A）^-1·4AE-2A=di

∵a+b=-3，ab=1，∴a、b同号，都是负数，∴ba+ab的值=-aba-abb=-1a-1b=-a+bab=-−31=3．

碰到这种问题不要偷懒,直接用待定系数法把B的9个元素设出来,然后乘开来比较等上面的做法做过一遍之后再做取巧一点的办法:(A-E)B=B(A-E),同样乘开来比较上面两个都做过之后可以设法去证明与Jor

（1）(2a+c)BC*BA+cCA*CB=0即:(2a+c)*[a*c*cosB]+c*[b*a*cosC]=0即:(2a+c)cosB+bcosC=0即：2acosB+(c*cosB+b*cosC

设B=b1b2b3b4因为AB=BA所以有b1+b3b2+b400=b1b1b3b3所以b1+b3=b1b2+b4=b1b3=0故B=a+ba0ba,b为任意常数

若AB是对称矩阵,则AB=(AB)^T=B^TA^T=BA若AB=BA,则AB=BA=B^TA^T=(AB)^T故AB是对称的.BA同理可得

∵a2+2a+b2-6b+10=0，∴a2+2a+1+b2-6b+9=0，∴（a+1）2+（b-3）2=0，∴a+1=0，b-3=0，∴a=-1，b=3，∴ba=3-1=-3；

7的倍数,在二位数中有14、21、28、35、42、49、56、63、70、77、84、91、98加1后得：15、22、29、36、43、50、57、64、71、78、85、92、99符合条件的只有2

等式A*BA=4BA-2E两边左乘A,右乘A^-1,得|A|B=4AB-2E.代入|A|=2得B=2AB-E所以(2A-E)B=E因为|E-2A|≠0所以2A-E可逆故B=(2A-E)^-1.

(10a+b)(10c+b)=(10b+a)(10b+c)得99(ac-b^2)=0b^2=ac由于abc都是个位数,且ac是平方数所以可以穷举a=b=c=1~9a=1,b=2,c=4a=4,b=2,

AB=(-5-3,7-(-4))=(-8,11)BA=-AB=(8,-11)

等式两边同时左乘A：|A|BA=2ABA-8A等式两边同时右乘A的逆：|A|B=2AB-8E这样解出B＝diag(2,-4,2)

待定系数算一下就知道了么,答案是a+ba,a和b任意实数.0

是38X83,a和b分别为3和8.解法：个位数是4,两个数相乘等于4的组合有1X4；2X2；3X8；4X6；那么就有14X41；22X22；38X83和46X64四种可能,前两种很容易排出了,后两种一

解由A*BA=2BA-8E得(A*-2E)BA=-8E,B=-8(A*-2E)-1A-1=-8[A(A*-2E)]-1=-8(AA*-2A)-1=-8(|A|E-2A)-1=-8(-2E-2A)-1=

【答案】3a^2-2b^2【解析】3A-2B=3·（a^2-2ba）-2·（-3ab+b^2）=3a^2-6ba-（-6ab+2b^2）=3a^2-6ba+6ab-2b^2=3a^2-2b^2(注意a

92+29=121