f(0)=ln(1 kx)m X

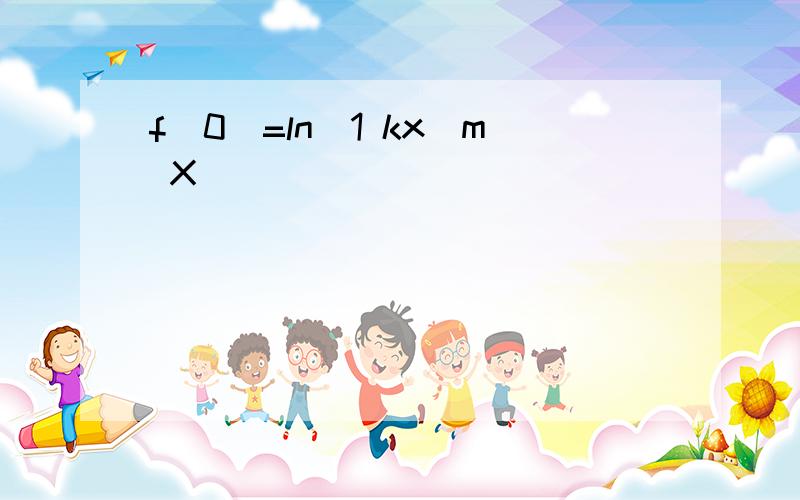
lnx求导是1/x这里用到了复合函数求导,就是y=f(g(x))y'=f'(g(x))*g'(x)具体一下就是f'(x)=e^x/(e^x+1)-ae^x+1在分母上.e^x+1求导是e^x,在分子上

f(x)＝ln(1+x)-kx当k=0时f(x)=ln(1+x)无最大值定义域为1+x>0x>-1当k≠0时求导f'(x)=1/(x+1)-k=(1-kx-k)/(x+1)=[-kx+(1-k)]/(

求导函数f′(x)=1/(x+1)+m．∵当x=0时,函数f（x）取得极大值∴f'（0）=0,得m=-1,此时f′(x)=-x/(x+1)．当x∈（-1,0）时,f'（x）＞0,函数f

f'(x)=1/(x+1)-k,f'(0)=0得,k=1.当0

（一元函数）可导,必定连续.显然f(x)在x=0处不连续.f(x)=ln(1+kx)-->0(x-->0)f(x)=-1(x=0)题目是不是给错了呀!

1、直接求导,令导数=0,此时x=12,解出K2、也就是说函数f的最大值在区域范围内,还是求导,令导数=0,将x用k表示,代入原函数f,得到最大值,此最大值>=x,而x又是k表示的,所以K范围出来了再

定义域x大于-0.5导函数1/(2x+1)-m导函数值域大于0,所以当m小于等于0的时候,导函数恒大于0,所以函数递增当m大于0的时候,x等于（1/2m-0.5)此时函数在x大于-0.5小于等于1/2

由等价无穷小的定义有：limln(1+kx)/(2x)=1而实际上ln(1+kx)等阶于kx所以上面的极限limln(1+kx)/(2x)=limkx/(2x)=k/2=1于是k=2

根据拉格朗日中值定理知,原命题等价于证明4/3再问：这也太专业了吧。。我们都没学这个。用高中知识把再答：简单的方法是有吧，不过我暂时没想出来，那需要巧妙的处理。高中这种题都被我跳过去了，没认真听。现在

Ⅰf(x)=ln(x+1)-x+x^2、f(1)=ln2,即切点为(1,ln2).f'(x)=1/(x+1)-1+2x、f'(1)=1/2-1+2=3/2,即切线斜率为3/2.所以,切线方程为：y-l

已知函数f(x)=ln(mx的二次方+mx+1)定义域为R,求实数m取值范围.（二次方吧）  m=0  f(x)定义域为R,满足条件m>0且判别式=m^2

变形:x/ln(x+1)-12令F(x)=ln(x+1)+4/(x+2)求导F'(x)=1/(x+1)-4/(x+2)^2=x^2/[(x+1)·(x+2)^2]>0(0

k^m再问：再答：那就不对了再问：恩再问：我想知道过程再答：mk再问：过程呐再答：lim(1+kx)^(1/kx)*mk再答：等于lne^mk再答：最后等于mk

用倒数的定义求x≠0时,令x→0,f'(x)=lim[f(0+x)-f(0)]/x=lim[ln(1+kx)/x-(-1)]/x=lim(k+1)/x.因f(x)在点x=0处可导,故极限存在,则k=-

楼主这么晚还没休息啊我想请问一下楼主的f(x)=ln(1+x)/x//ln(1+x)是从网上看到的?还是从书本上看到的?而且,我认为,楼主f(x)=ln(1+x)/x//ln(1+x)打多了一个除号,

f(-x)=-kx+ln(e(-x)+1)=-kx+ln(e^x+1)-lne^x=-(k+1)x+ln(e^x+1)=f(x)=kx+ln(e^x+1)-(k+1)x=kx-(k+1)=kk=-1/

因为lnx是增函数所以当x=1时g(x)=kx+1/x取极小值g'（x）=k-1/x^2所以当x等于根号k时取最小值即=1再问：上面是(kx+1)/x再答：是ln[(kx+1)/x]?(kx+1)/x

是f(x)=（ln(1+kx)）^m/x还是f(x)=ln（(1+kx)^m）/xf(0)=m*k