limx->0 1 cosx^3=-搜答案-大师作文网

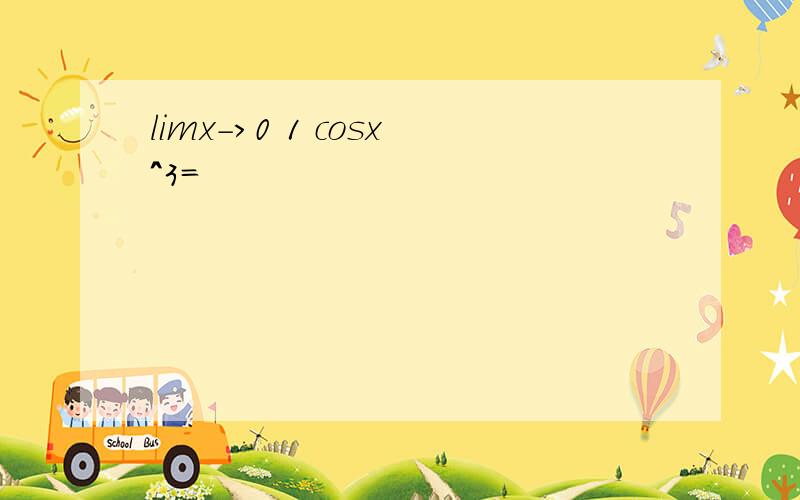
原式=e^[lim(x->0)(lncosx)/x]=e^[lim(x->0)(1/cosx×(-sinx))/1]=e^[lim(x->0)-tanx]=e^0=1

应该是趋近于0吧!

(用等价无穷小量求解)　　x→0时:1-cosx～(1/2)x^2　　ln(1+x)～x　　tanx～x　　所以所求极限是1/2　　希望对你有点帮助!

x趋向于0时,1-cosx等价无穷小是1/2x^2所以,原极限就等价于求解limx趋向于0xf(x)/(1/2x^2)=limx趋向于02f(x)/x因为f(x)连续可导,f(0)=0,f'(0)=3

secx-cosx=1/cosx-cosx=(1-cos^2x)/cosx=(1+cosx)(1-cosx)/cosx所以原式=limcosxln(1+x^2)(1+cosx)(1-cosx)x趋于0

第一个是在0/0情况下直接应用洛必达法则,分子分母同时求导得到的第二个是分子中的单项sinx~x,分母中括号里的东西不是趋向于0,而是趋向于2,因此直接取为2

使用罗比达法则lim(x->0)(2/3*(1+2x)^(-2/3))/(sinx+cosx)=2/3

-1/30BUCUNZAIBUCUNZAI1

因为3sinx-2cosx=0,所以sinx/2=cosx/3.令sinx=2k,cosx=3k,k≠0.(1)原式=(3k-2k)/(3k+2k)+(3k+2k)/(3k-2k)=(1/5)+5=2

等于1,用罗比达法则求第一步：等于[1-1/(1+x)]/sinx的极限,第二步就可以得到结果了

limx->0[tanx-sinx]/sinx^3===>limx->0[tanx-sinx]/x^3===>limx->0[tanx(1-cosx)]/x^3===>limx->0[(tanx/x)

x趋于零时,1-cosx等价于x^2/2,直接就可得出答案是1/2,这是考研的送分题呀!再说明白点,1-cosx=1-(1-2(sin(x/2))^2)=2sin(x/2)^2等价于x^2/2.老兄,

=e^lim(1/sin²x)·lncosx=e^lim(cosx-1)/x²=e^lim-(1/2)x²/x²=e^-(1/2)

先计算极限lim(cosx+sinx+x^3)/x.以下过程如图.计算中使用了洛比达法则（图中第二行）,用了“有界函数乘以无穷小函数的极限认为无穷小”（第三、四、五行）

lncosx～cosx-1～-x/2设t=lncosx/x,limt=-1/2.原式=lime^4t=e^(-2)

解析：上下同时除以x,得原式＝lim(x→∞)(1＋2sinx/x)(3＋4cosx/x)＝(1＋0)/(3＋0)＝1/3.（因为x→∞,所以1/x→0,而sinx和cosx为有界函数,所以sinx/

替换原则：（1）首先要保证当x趋于某一个常数时,函数是无穷小量（2）加减不能替换,乘除能替换；（3）看代换后四则运算下来的最小量的阶是否与分母可比 &nb