设y=sin(x y),求dx分之dy-搜答案-大师作文网

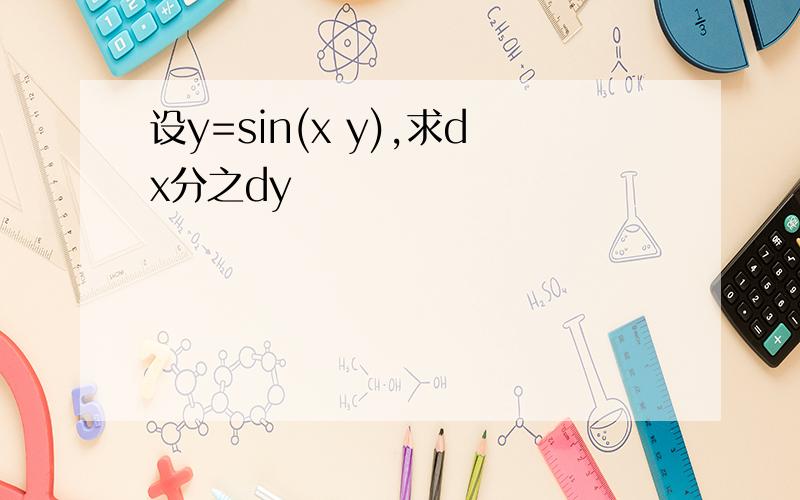
将y看成是关于x的函数即y=f(x)我们在求导的同时要记得y也要对x求导即dy/dx我们两边分别对x求导得e^x+e^y*dy/dx=cos(xy)*(y+x*dy/dx)移项e^x-y*cos(xy

再答：再问：再问：拜托了

1)x=0代入方程：1-e^y=0,得y(0)=0两边对X求导：e^x-y'e^y=cos(xy)(y+xy')y'=[e^x-ycos(xy)]/[xcos(xy)+e^y]代入x=0,y(0)=0

e^(x+y)-xy=1两边同时求导,e^(x+y)*(1+dy/dx)-y-xdy/dz=0(1)验证x=0,y=0在原曲线上.令x=0,y=0代入到（1）e^0*(1+dy/dz)-0-0*dy/

再答：隐函数高阶求导。再答：

e^(xy)+sin(xy)=y(y+xy')e^(xy)+(y+xy')cos(xy)=y'y'=(ye^(xy)+ycos(xy))/(1-xe^(xy)-xcos(xy))

满意请采纳,谢谢

这个题目要利用隐函数的求导法则.则sin(x^2+y)=xy（两边同时求导,还要结合复合函数的求导法则）cos（x^2+y）*（2x+y′）=y+xy′2xcos（x^2+y）-y=xy′-y′cos

z=arctan(x*e^x)z'={1/[1+(x*e^x)^2]}*(x*e^x)'(x*e^x)'=x'*e^x+x*(e^x)'=e^x+x*e^x=(x+1)*e^x所以dz/dx=(x+1

cos(x+y)(1+y')=y+xy'dy/dx=y'=[y-cos(x+y)]/[cos(x+y)-x]

y=sin(xy)dy/dx=cos(xy)*y=ycos(xy)d²y/dx²=-ysin(xy)*y=-y²sin(xy)

三种方法1式中同时对x求导-（y+xy‘）cosxy+2yy'=0解出y’2式中同时取微分d{sin(xy)+y^2-e^2}=dsin(xy)+dy^2-de^2=-cosxydxy+2ydy=-c

等式两边对x求导：cos(xy)*(y+x*y')-(2x*2y+x^2*2*y'=0解出y'即为所求

请参照图片

你好!两边对x求导：e^(xy)*(y+xy')-y^2=y'cosy解得y'=(y^2-ye^(xy))/(xe^(xy)-cosy)

y+xy'-cos(πy²)2πyy'=0y=[2πycos(πy²)-x]y'y'=y/[2πycos(πy²)-x]即：dy/dx=y/[2πycos(πy²

∵siny＋e^x－xy^2＝0,∴（dy/dx）cosy＋e^x－［y^2＋2xy（dy/dx）］＝0,∴（cosy－2xy）（dy/dx）＝y^2－e^x,∴dy/dx＝（y^2－e^x）/（co

sin(xy)=x 求dx/dy

x/[sec(xy)-y]dx/dy.

（cos（x+y）-y）\(x-cos(x+y))

dy/dx=-fx/fy,你自己可以算吧