yz xy xz=1 z=f(x,y)

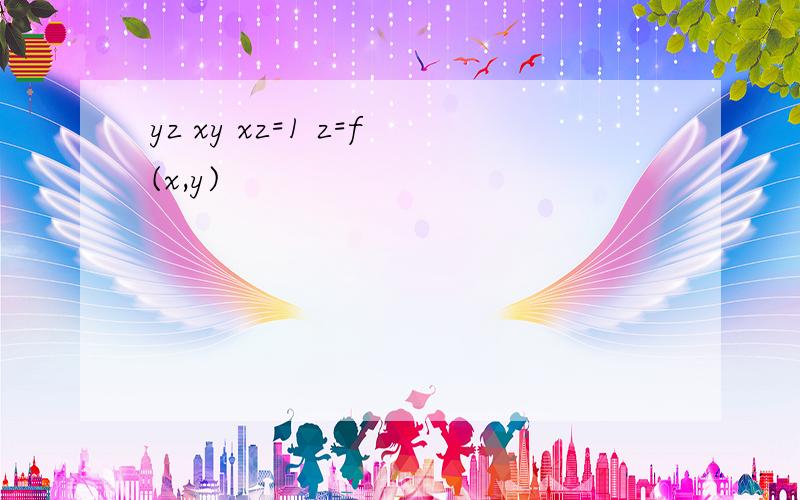
二重积分,画出积分区域,分段积分就行

这是复合函数的导函数的利用δz/δx=2xyf'/f²δz/δy=[f+yf'(-2y)]/f²=(f-2y²f')/f²1/x×δz/δx+1/y×δz/δy

由已知得到：lg(1+x)/(1-x)+lg(1+y)/(1-y)=lg(1+z)/(1-z)即lg(1+x)(1+y)/(1-x)(1-y)=lg(1+z)/(1-z)即(1+x)(1+y)/(1-

(太麻烦拉,给点分啊!)设v=x*x-y*y,u=exp{xy}那么dv/dx=2x(这里应该用偏导符号,代替一下),dv/dy=2y,du/dx=y*exp{xy},du/dy=x*exp{xy}那

G[x+z*y^(-1),y+z*x^(-1)]=0证明x*∂z/∂x+y*∂z/∂y=z-xy?Gz=(1/y)G1+(1/x)G2=LGx=G1-(

f(x,y,z)=yz+xz使得,y^2+z^2=1,yz=3令F(x,y,z)=yz+xz+a(y²+z²-1)+b(yz-3)Fx=z=0Fy=z+2ay+bz=0Fz=y+x

1、由单变元的微分中值定理,有f(x,y)－f(x0,y)＝f'x(c,y)*(x－x0)＝0,于是f(x,y)的值只与y有关,故z＝f(y).2、由1知道,当f'xy(x,y)＝0时,f'y(x,y

%单纯从定义上没有错误,但是如果计算时xyz是数组或向量时就会报错,因为要求加点运算%试改为：f=@(x,y,z)(1+y).*z.^y-(-0.25*(x-1).^2+0.25).^x看看

两边对x求导1-a*δz/δx=f'(y-bz)*(-bδz/δx)整理得：[a-bf'(y-bz)]δz/δx=-1两边对y求导-a*δz/δy=f'(y-bz)*(1-bδz/δy)整理得：[-a

f对第1个变量的偏导函数记作f1,第2个变量的偏导函数记作f2,dz=f1*d(xz)+f2*d(z/y)...[注：写完整的话是f1(xz,z/y),f2也如此]=f1*(xdz+zdx)+f2*(

令(y+z)/(1+yz)=X1,(y-z)/(1-yz)=X2,因为f(x)=lg((1+x)/(1-x))所以f(X1)=lg((1+X1)/(1-X1)=1,f(X2)=lg((1+X2)/(1

再问：是否还能给出一种利用题目所给的条件(关于x,y,z的函数)去证明的方法吗？再答：这就是课本上隐函数求导公式的应用，你想得太多了，没有必要的！

把代码补全一点,主要是注意返回类型!#include"stdio.h"intz=5;voidf(){staticintx=2;inty=5;/*x为静态变量,分配了以后直到程序结束,y没实际用到*/x

f(x)=lg[(1-x)/(1+x)]f(y)=lg[(1-y)/(1+y)]f(x)+f(y)=lg[(1-x)/(1+x)]+lg[(1-y)/(1+y)]=lg[(1-x)(1-y)/(1+x

1、隐函数对x求导得1+az/ax+yz+xy*az/ax=0,故az/ax=－(1+yz)/(1+xy)；F对x求导得aF/ax=e^x*y*z^2+e^x*y*2z*az/ax；当x＝0,y＝1时

分别把x,y,z,t当做为之数,其余都是常数,求就行了再问：具体怎么做呢？麻烦写清楚些

=x²(y-z)+y²(z-x)+z²(x-z+z-y)=(y-z)(x²-z²)+(z-x)(y²-z²)=(y-z)(x-z)

f=x+1f+u=2x+3f+u+c=3x+8f+u+c+k=4x+15f(f,u,c,k)=(x+1)(2x+3)(3x+8)(4x+15)

1.用拉格朗日乘数法没有用柯西不等式的方便(x²+y²+z²)*(1+1+1)≥（x+y+z)²=1当x=y=z时等号成立所以x²+y²+z