√1-x -3 2 ³√ x

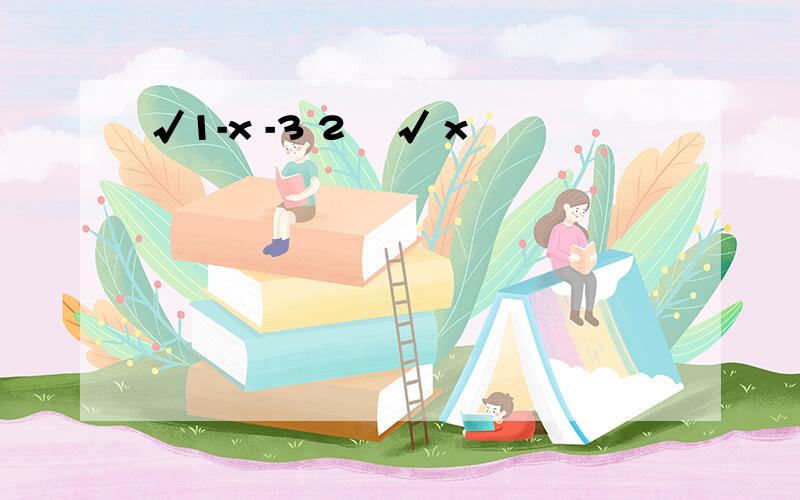
y=x^(7/6)+x^(-7/6)y`=7/6x^(1/6)-7/6x^(-13/6)

y'=6x^2-3+1/(2√x)+3/2*x^(-5/2)再问：������Ŀɲ�����дһ�¹����������再答：��ָ����再问：恩恩，知道，可是中间过程不知如何下笔，请指点，可以化简

答：设t=√(x-2)>0,x=t^2+2,dx=2tdt原式=∫{x+1/[x√(x-2)]}dx=∫{t^2+2+1/[(t^2+2)t]}2tdt=∫(2t^3+4t)dt+2∫1/(t^2+2

你那个公示表达我看不大懂,如果式子跟我写的一样,那就是这样啦,传个照片好麻烦.希望能帮到你

x(x+1)-x-9=0x²+x-x-9=0x²-9=0(x-3)(x+3)=0x=3或x=-3x²-2x=224x²-2x-224=0(x-16)(x+14)

y/x哪个是分子?按理说y/x应该是x分之y,即y是分子再问：x是分子啊二次根式化简。。。。再答：注意应是分子/分母分子在前面的我前面都是按这个做的显然x>0,y>0则原式=(2x/3)*3√x+6x

由x-x²≥0,得函数定义域为：[0,1]配方,得：x-x²=-(x-1/2)2+1/4所以,得：0≤x-x²≤1/4所以,函数f(x)=√x-x²的值域为：[

limx[(√x^2+1)-x=limx[(√x^2+1)-x]*[(√x^2+1)+x]/[(√x^2+1)+x]x→+∞x→+∞=limx/[(√x^2+1)+x]x→+∞=limx*(1/x)/

f(x)=ln(x+√1+x^2)f'(x)=1/(x+√(1+x^2)*(x+√1+x^2)'=1/(x+√(1+x^2)*(1+(√1+x^2)'=1/(x+√(1+x^2)*(1+1/2*√(x

√(x+1)-√x=(√(x+1)-√x)(√(x+1)+√x)/(√(x+1)+√x)=(x+1-x)/(√(x+1)+√x)=1/(√(x+1)+√x)->0（x→+∞）arccos（1-x)的x

1直接把0+代入就行了,指数部分我认为根号下是x/1-x,则极限=1/22中括号的右括号我认为在末尾.也是一个直接代入x=0即可得题目,极限=1

x*x-3x+1=0x*x+1=3x√(x*x+1/x-2)=√(3x/x-2)=√（3-2)=1再问：/是除号再答：是的啊再问：应是x*x+1除以x-2再答：如果是这样的话，你把x=（3+根号5）/

分步写,好让看的清楚符号[√(x^2-6x+9)/x^2-x-12]=√(x-3)^2/(x-4)(x+3）=（x-3)/(x-4)(x+3）；(x^3-16x)/(x^2-3x)=x(x^2-16)

一步一步微分、积分并用,就可以还原出原函数,也就是一些教师所说的“还原法”,或“凑微分法”：∫(arctan√x)/[√x×(1+x)]dx=2∫(arctan√x)/[1+x]d√x=2∫(arct

1.定义域x>0,f'(x)=1/(2√x)+1/x^2>0,f(x)在定义域上是增函数也可以用定义证明.设h>0,f(x+h)-f(x)=[√(x+h)-1/(x+h)]-[√x-1/x]=[√(x

提示：有个公式：(1+x)^α=1+αx+α(α-1)x^2/2!+α(α-1)(α-2)x^3/3!+.在上面展开式中,你用-1/2代α,用-2x代x,最后各项再乘以x就行了.

分成∫dx/√(x-2)和∫dx/[x√(x-2)].第一部分相信楼主肯定会,第二部分设u=√(x-2),代换就成了.希望楼主满意.

lim(x→1)[√(3-x)-√(1+x)]/(x^2+x-2)=lim(x→1)[√(3-x)-√(1+x)])[√(3-x)+√(1+x)]/{(x^2+x-2)[√(3-x)+√(1+x)]}

（-x+√x²+1)=(-x+√x²+1)(x+√x²+1)/(x+√x²+1)=[(√x²+1)²-x²]/(x+√x²