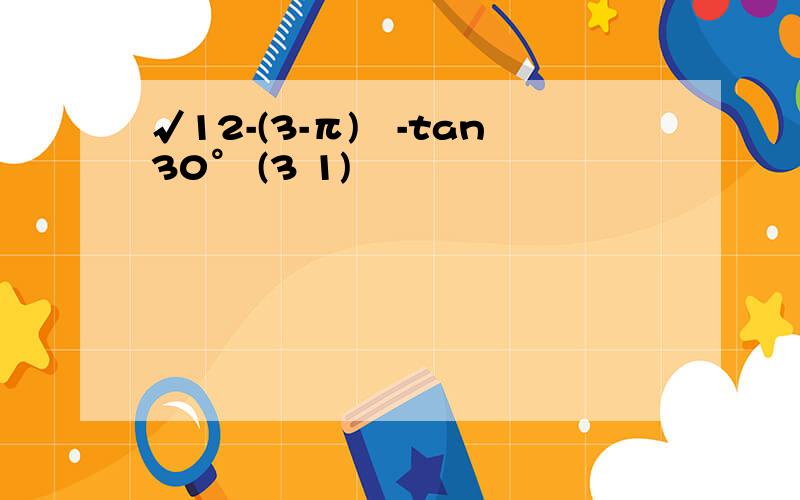
√12-(3-π)º-tan30° (3 1)

利用诱导公式tanx=tan（x+π）π≈3.14π/2≈1.57tan2=tan（2-π）=tan(-1.14)tan3=tan(3-π）=tan（-0.14）tan4=tan（4-π）=tan0.

tan89=cot(90-89)=cot1=1/tan1所以tan1*tan89=1同理tan2*tan88=1……tan44*tan46=1tan45=1所以原式=1

1π/3再问：第三个应该是log1/2tan(70°)＜log1/2(cos(25°))＜log1/2(sin(25°))，你再看看再答：是的，不好意思，笔误了都说了是减函数了：故：tan(70°)>

显然,tan1>0,tan2tan3主要判断工具是单位圆～～

-1/tan3=-ctg3=ctg(-3)=tg(3+pie/2)=tg(3-pie/2)所以A＝3-pie/2+n*pie

确定三角函数的符号,关键是看三角函数作用的角在哪个象限这里说的是弧度4弧度=4*180/pi度=229.1831度sin4=-0.75682弧度=2*180/pi度=114.5916度cos2=-0.

（1）tan1ºtan2ºtan3º...tan89º=(tan1º*tan89º)(tan2º*tan88º)(tan

tan[arctan(-√3/3)]tan(-π/6)=-√3/3所以tan[arctan(-√3/3)]=tan(-π/6)=-√3/3arctan(tan3π/4)=arctan(-1)=-π/4

∵23°+37°=60°，tan60°=3∴tan（23°+37°）=tan23°+tan37°1-tan23°•tan37°=3，去分母整理，得tan23°+tan37°=3-3tan23°tan3

sinα·tanα＜0cosa

证明：3+tan1°•tan2°+tan2°•tan3°=（1+tan1°•tan2°）+（1+tan2°•tan3°）+1=tan2°−tan1°tan(2−1)°+tan3°−tan2°tan(3

因为0再问：在三角形ABC中向量AB=向量a向量AC=向量bAP的中点为QBQ的中点为RCR的中点为P使用向量a、b表示向量AP

 再答：移到同一周期才好比较

tan里面只有一,三象限是正数,其他都是负数.sin里面一,二象限是正数,其他是负数.cos里面一,四象限是正数,其他是负数.建议你先画一个坐标图,然后根据坐标图判断个角度的位置,离最大值近的大.ta

1=tan45=tan(1+44)=(tan1+tan44)/(1-tan44)所以1-tan1*tan44=tan1+tan44其它类似,即1-tanx*tan(45-x)=tanx+tan(45-

3+tan1°tan2°+tan2°tan3°=(1+tan1°tan2°)+(1+tan2°tan3°)+1=(1+tan2°tan1°)+(1+tan3°tan2°)+1=(tan2°-tan1°

1-2sin^24β=cos8βsin^25β-cos^25β=1-cos^25β-cos^25β=1-2cos^25β=-cos10β1-tan^23β=2tan3β/tan6βtan3β/1-ta

(1)f(x)=【1-sin(x-3π/2)+cos(x+π/2)+tan3π/4】/cosx=【1-sin(x+π/2)+cos(x+π/2)-1】/cosx=[-cos(-x)+sin(-x)]/

A=100B=200C=S.B分之2.B

1=57.3度依次类推2=114.6度3=171.9度因为tan函数是递增函数,所以tan3大于tan2结果正确,过程值得商榷.tan函数是增函数是有条件的,在某一个定义域中是这样的.