∠ABC=100 ∠C的平分线交AB边于点E 在AC边
来源:学生作业帮助网 编辑:作业帮 时间:2024/11/19 18:06:22
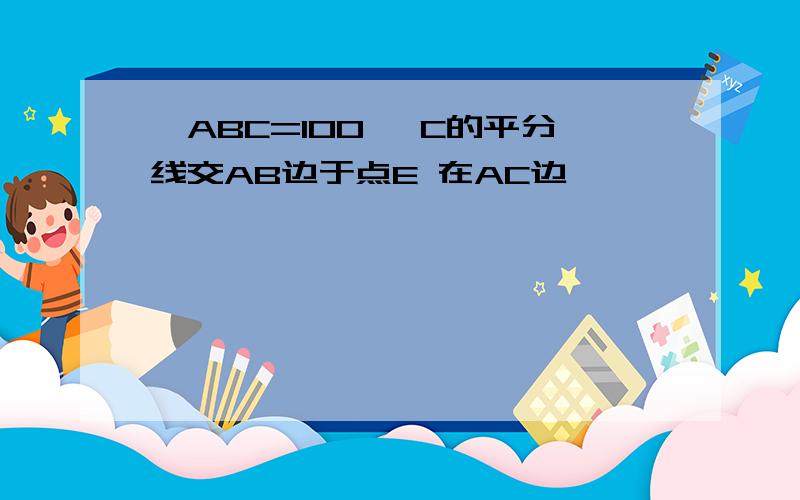
证明:∵BE是∠ABC的平分线∴∠CBE=∠EBF又∵BE⊥CF∴CE=EF,CF=2CE,∠EBF+∠F=90°∵BF⊥CA∴∠ACF+∠F=90°∴∠EBF=∠ACF∵AB=AC∴△BAD≌△CA
由于我不会几何画图工具,所以有关的辅助线你得自己在图上画一下!延长CE交BA的延长线与点F证明:∵∠ABC的平分线交AC于D,∴∠FBE=∠CBE,∵BE⊥CF,∴∠BEF=∠BEC,在△BFE和△B
(1)∠A=180°-∠ABC-∠ACB=180°-(180°-100°)X2=20°第二题的题目应该打错了,应该是"分别交于AB,AC于EF两点“,不然不合理.由于EF∥BC,所以,∠EDB=∠DB
解题思路:根据内角和定理解答解题过程:varSWOC={};SWOC.tip=false;try{SWOCX2.OpenFile("http://dayi.prcedu.com/include/rea
设E为AB延长线上的一点因为∠CBE=∠C+∠CAB,∠CBD=∠DBE,∠CAD=∠DAB所以∠DBE=1/2∠C+∠DAB而∠DBE=∠D+∠DAB所以∠D=1/2∠C=35°
(1)∠BGC+∠GBC+∠GCB=180°∠GBC=1/2∠ABC∠GCB=1/2∠ACB代入有∠BGC+1/2∠ABC+1/2∠ACB=180°即∠BGC=180°-1/2(∠ABC+∠ACB)(
因为2∠CBD=180°-∠ABC所以∠CBD=90°-∠ABC/2因为∠D=180°-∠BAD-∠ABC-∠CBD=180°-∠BAD-∠ABC-(90°+∠ABC/2)2∠D=180°-2∠BAD
证明:因为AB=AC,所以角ABC=ACB,因为CF,BE是角平分线,所以角ACF=FCB=EBA=角EBC,所以角AFC+角FAE=角ABC+FCB+FCA+BAC=180所以AE平行FC,同理FA
结论:四边形AFDE是菱形.证明:∵∠ABC=∠ACB,∠ABE=∠EBC=∠ACF=∠FCB.又∠FAB、∠FCB是同弧上的圆周角,∴∠FAB=∠FCB,同理∠EAC=∠EBC.有∠FAB=∠ABE
∠DCE=∠ACD=0.5∠ACE∠DCE=0.5∠B+∠D∠ACE=∠B+∠A=2∠DCE=∠B+2∠D解得∠D=0.5∠A答案也是(1/2)
90或135度详情请画图
∠D的度数为:70/2=35°.设,∠CAD=∠DAB=∠1,∠CBD=∠DBE=∠2.∠ABC=180-(∠C+2∠1),而,∠ABC=180-2∠2,则有∠C+2∠1=2∠2,∠2-∠1=∠C/2
1.EF‖AC,∠BFG=∠A.∠A+∠ACD=∠BCD+∠ACD=90,所以∠BCD=∠A=∠BFG,BG=BG,∠CBG=∠FBG△BFG≌△BCG,BF=BC2.BF=BC,∠CBG=∠FBG,
(1),BE,CF分别为∠b和∠c的角平分线,交于点G,∠GBC=二分之一∠ABC,∠GCB=二分之一∠ACB,∠BGC=180°-∠GBC-∠GCB=180°-二分之一∠ABC-二分之一∠ACB=1
∠BEC=90+1/2×70=125∠BFC=1/2×(180-70)=55
如图 在三角形ABC中∠A=60°∠B+∠C=120°∵∠B,∠C的平分线交于P ∴∠BPC=180°-1/2(∠B+∠C)=120°∵∠E+∠PCE=∠BPC=120°CE平分∠
由已知得:△ABC与△ADE相似所以AE/AC=DE/BC又因为DE平行于BC所以∠EDC=∠DCB又因为DC平分ACB所以∠DCB=∠ACD所以∠EDC=∠ACD所以ED=CE故DE/BC=AE/A
115°延长BA,做PN⊥BD,PF⊥BA,PM⊥AC,设∠PCD=x°,∵CP平分∠ACD,∴∠ACP=∠PCD=x°,PM=PN,∵BP平分∠ABC,∴∠ABP=∠PBC,PF=PN,∴PF=PM
证明:因为∠A的平分线AD交BC于D,BP⊥AD,所以△ABE为等腰三角形,所以AE=AB设∠AEB=z度,∠EBC=y度,∠C=x度,则∠ABC=3x度于是z=x+y,z=3x-y整理得x=y,则B
∵DE∥BC,∴∠1=∠3.又∠1=∠2,∴∠2=∠3DE=EC由△ADE∽△ABC,∴DEBC=AEAC,DEa=b−DEb,b•DE=ab-a•DE,故DE=aba+b.