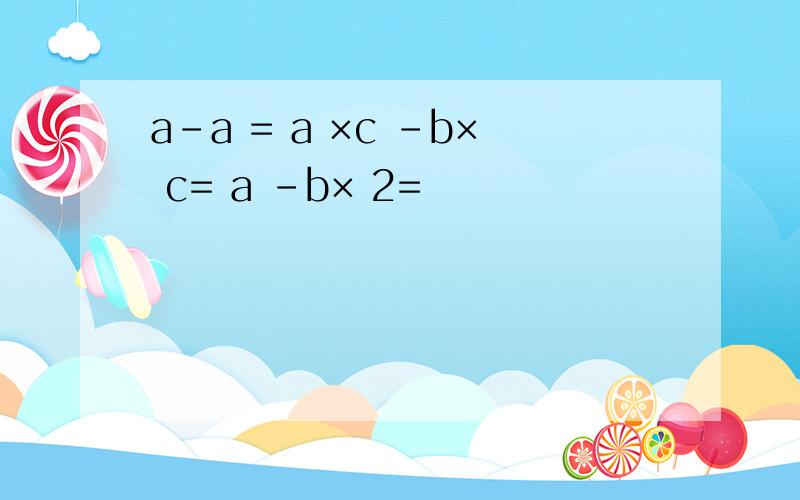a-a = a ×c -b× c= a -b× 2=

行列式证明|b+c c+a a+b| | a b c||a+b b+c c+a| = 2 |c a b||c+a a+b (a-b-c)(b+c-a)(c-a+b)= A B C A=( ) 为什么[(a+b)^2-c^2)][(a-b)^2-c^2)]=(a+b+c)(a+b-c)(a-b+c)(a-b-c) 已知a,b,c是正数,求证a^2a*b^2b*c^2c>=a^(b+c)*b^(c+a)*c^(a+b) 已知(b+c)/(a)=(c+a)/(b)=(a+b)/(c) 求(a+b)/(c) 证明 +(a-b)(b-c)(c-a)/(a+b)(b+c)(c+a)=0 (a-b)b+c(b-a)=c(c-a)+b(a-c)? a+b+c=0,abc求a(b+c)+b(a+c)+c(a+b) [(a-b)(b-c)(c-a)]÷[(a-c)(c-b)(b-a)]= 若a/b+c=b/c+a=a+c/a+b+2c,则a：b= 已知a+b+c=0求证:(a-b/c+b-c/a+c-a/b)(c/a-b+a/b-c+b/c-a)=9