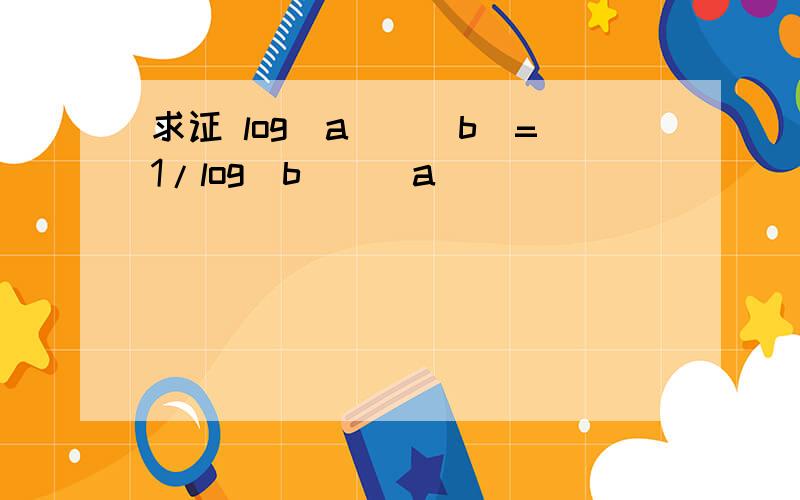
求证 log(a)^(b)=1/log(b)^(a)

求证：log底数a真数b=1/log底数b真数a log a b*log b c=log b b*log a c成立吗 log(ab)=log(a)+ log(b)吗 利用换底公式证明：log(a)b.log(b)c.log(c)a=1 设a>b>1,log(a)b+log(b)a=10/3,则log(a)b-log(b)a= 已知a大于b大于1,log(a)b+log(b)a=10/3,求log(a)b-log(b)a的值 已知a＜b＜1,log(a)b+log(b)a=10/3,求log(a)b-log(b)a的值 log a b=log b a,则：ab=? 公式：log(a)(b)*log(b)(a)=? 化简log(1/a)b+log(a)b a^[log(a)b×log(b)c×log(c)N] 证明：log(A)M=log(b)M/log(b)A (b>0且b≠1）.