∫(0→π)√(sin∧3 x-sin∧5 x)dx
来源:学生作业帮 编辑:大师作文网作业帮 分类:数学作业 时间:2024/11/19 09:49:00
∫(0→π)√(sin∧3 x-sin∧5 x)dx
正确答案是4/5,如果令sinx=t,x=0→t=0,x=π,t=0,后面直接不用看,∫(0→0)=0有人说连续导数是导数无拐点,sinx导数cosx在[0,π]有拐点,不连续,不能用换元法?
正确答案是4/5,如果令sinx=t,x=0→t=0,x=π,t=0,后面直接不用看,∫(0→0)=0有人说连续导数是导数无拐点,sinx导数cosx在[0,π]有拐点,不连续,不能用换元法?
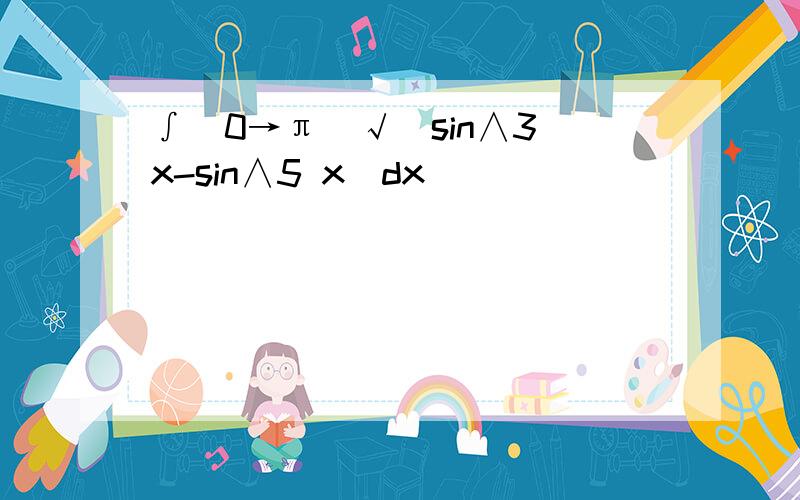
如果按你说的 用 换元法 做的话,t ∈ [0,1] 同时 x=arcsint
dx=1/√1+t^2 岂不是麻烦了
在我看来,没有什么比按部就班来的快
积分式 =cosx sin(^3/2)x=(2/5)sin(^5/2)x 在积分域上 sinx ∈ [0,1]
x∈[0,π/2] sinx的积分 =1 同理 x∈ [π/2,π] sinx的积分=1
snx在x∈[0,π]均在x轴上方 应该相加的
所以 =2/5 *2= 4/5
如有不懂的,请追加
dx=1/√1+t^2 岂不是麻烦了
在我看来,没有什么比按部就班来的快
积分式 =cosx sin(^3/2)x=(2/5)sin(^5/2)x 在积分域上 sinx ∈ [0,1]
x∈[0,π/2] sinx的积分 =1 同理 x∈ [π/2,π] sinx的积分=1
snx在x∈[0,π]均在x轴上方 应该相加的
所以 =2/5 *2= 4/5
如有不懂的,请追加