作业帮 > 数学 > 作业

如图所示，△ABC是正三角形，△A1B1 C1的三条边A1B1、BlC1、C1A1交△ABC各边分别于C2、C

来源：学生作业帮 编辑：大师作文网作业帮 分类：数学作业 时间：2024/11/13 22:52:06
如图所示，△ABC是正三角形，△A1B1 C1的三条边A1B1、BlC1、C1A1交△ABC各边分别于C2、C3，A2、A3，B2、B3．已知A2C3=C2B3=B2A3，且C2C32+B2B32=A2A32．请你证明：AlB1⊥C1A1．
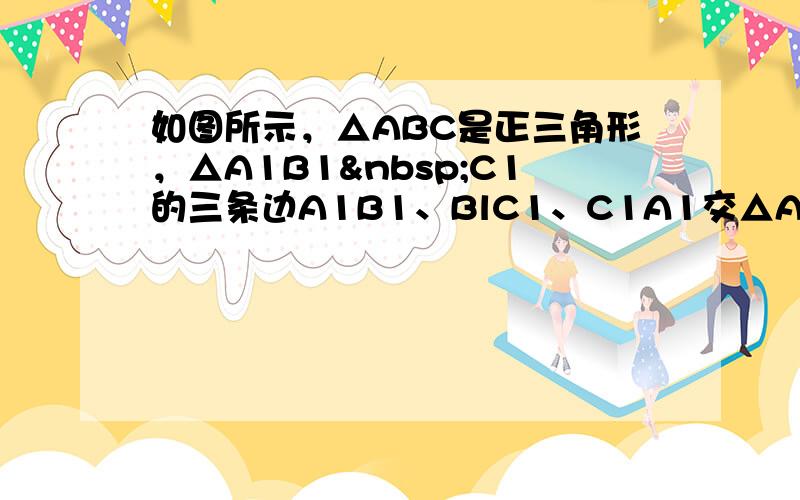
如图所示，△ABC是正三角形，△A1B1 C1的三条边A1B1、BlC1、C1A1交△ABC各边分别于C2、C
证明：如图，过A2作C3C2的平行线交过C2所作C3A2的平行线于点O，连接OA3、0B3，
∴A2OC2C3是平行四边形，
∴A2O∥C3C2，且A2O=C3C2，OC2∥A2C3且OC2=A2C3=B3C2，
∴△OB3C2是正三角形，
∴∠OB3C2=60°=∠B，
∴OB3∥A3B2，
又∵0B3=B3C2=A3B2，
∴OB3B2A3是平行四边形，
∴OA3∥B3B2且OA3=B3B2，
∵C2C32+B2B32=A2A32，
∴OA22+OA32=A2A32，
在△A2OA3中，
∵OA22+OA32=A2A32，
∴由勾股定理的逆定理得∠A2OA3=90°，
∵已证OA3∥B3B2，即OA3∥A1C1，A2O∥C3C2，即A2O∥B1A1，
∴∠C1A1B1=90°，
∴A1B1⊥C1A1．
三角形ABC是正角形,三角形A1B1C1的三条边A1B1、B1C1、C1A1交三角形ABC各边于C2C3A 18．如图,△ABC的面积为1．分别倍长AB,BC,CA得到△A1B1C1．再分别倍长A1B1,B1C1,C1A1得到△ 如图,△ABC的面积为1,分别倍长AB,BC,CA得到△A1B1C1,再分别倍长A1B1,B1C1,C1A1得到△A2B 已知在△ABC和△A1B1C1中,AB=A1B1,BC=B1C1,高BD=B1D1,则角C和角C1的关系是 如图所示,A1,B1,C1分别是△ABC的三边中点 A2,B2,C2 分别是△A1B1C1的各边的中点.是第一幅图. 如图所示,A1,B1,C1分别是△ABC的三边中点 A2,B2,C2 分别是△A1B1C1的各边的中点 已知如图,AD、A1D1分别是△ABC与△A1B1C1的中线,且AB:A1B1=BC:B1C1=AD:A1D1求证△AB 如图,AD和A1D1分别是△ABC和△A1B1C1的中线,且AB/A1B1=AC/A1C1=AD/A1D1,试判断△AB 已知:如图,AD、A1D1分别是△ABC与△A1B1C1的中线,且AB/A1B1=BC/B1C1=AD/A1D1,求证； 已知:如图,AD,A1D1分别是△ABC和△A1B1C1的中线,且AB/A1B1=BC/B1C1=AD/A1D1.求证: 已知:△AD A1D1分别为锐角△ABC和△A1B1C1的边BC B1C1的中线 且AB=A1B1 AD=A1D1请你补 ⊙O与△ABC的三边BC、CA、AB分别交于点A1、A2、B1、B2、C1、C2,过上述六点分别作所在边的垂线a1、a2