已知:△ABC内接于⊙O,过点A作直线EF.
来源:学生作业帮 编辑:大师作文网作业帮 分类:数学作业 时间:2024/11/10 21:48:09
已知:△ABC内接于⊙O,过点A作直线EF.
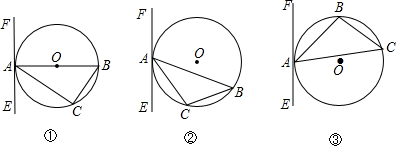
(1)如图①,AB为直径,要使EF为⊙O的切线,还需添加的条件是(只需写出三种情况):
① ___ ;② ___ ;③ ___ .
(2)如图②,AB是非直径的弦,∠CAE=∠B,求证:EF是⊙O的切线.
(3)如图③,AB是非直径的弦,∠CAE=∠ABC,EF还是⊙O的切线吗?若是,请说明理由;若不是,请解释原因.

(1)如图①,AB为直径,要使EF为⊙O的切线,还需添加的条件是(只需写出三种情况):
① ___ ;② ___ ;③ ___ .
(2)如图②,AB是非直径的弦,∠CAE=∠B,求证:EF是⊙O的切线.
(3)如图③,AB是非直径的弦,∠CAE=∠ABC,EF还是⊙O的切线吗?若是,请说明理由;若不是,请解释原因.

(1) 当AB⊥EF或∠BAE=90°可判断EF为⊙O的切线;
当∠ABC=∠EAC,∵AB为直径,
∴∠ACB=90°,
∴∠ABC+∠CAB=90°,
∴∠EAC+∠CAB=90°,
∴AB⊥EF,
∴EF为⊙O的切线;
故答案为AB⊥EF、∠BAE=90°、∠ABC=∠EAC;
(2)证明:如图2,作直径AD,连结CD,
∵AD为直径,
∴∠ACD=90°,
∴∠D+∠CAD=90°,
∵∠D=∠B,∠CAE=∠B,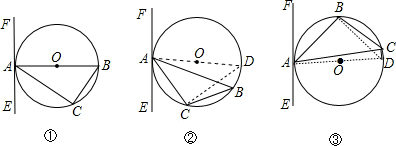
∴∠CAE=∠D,
∴∠EAC+∠CAD=90°,
∴AD⊥EF,
∴EF为⊙O的切线;
(3)如图3,作直径AD,连结CD,BD,
∵AD为直径,
∴∠ABD=90°,
∵∠CAE=∠ABC,
∴∠DAE+∠DAC=∠ABD+∠DBC,
而∠DAC=∠DBC,
∴∠DAE=∠ABD=90°,
∴AD⊥EF,
∴EF为⊙O的切线.
当∠ABC=∠EAC,∵AB为直径,
∴∠ACB=90°,
∴∠ABC+∠CAB=90°,
∴∠EAC+∠CAB=90°,
∴AB⊥EF,
∴EF为⊙O的切线;
故答案为AB⊥EF、∠BAE=90°、∠ABC=∠EAC;
(2)证明:如图2,作直径AD,连结CD,
∵AD为直径,
∴∠ACD=90°,
∴∠D+∠CAD=90°,
∵∠D=∠B,∠CAE=∠B,

∴∠CAE=∠D,
∴∠EAC+∠CAD=90°,
∴AD⊥EF,
∴EF为⊙O的切线;
(3)如图3,作直径AD,连结CD,BD,
∵AD为直径,
∴∠ABD=90°,
∵∠CAE=∠ABC,
∴∠DAE+∠DAC=∠ABD+∠DBC,
而∠DAC=∠DBC,
∴∠DAE=∠ABD=90°,
∴AD⊥EF,
∴EF为⊙O的切线.
已知:△ABC内接于圆O,过点A作直线EF.若直线AB是非直径的弦,∠CAE=∠B,求证:EF是圆O的切线.
如图,△ABC内接于⊙O,AB是直径,过点A作直线MN,若∠MAC=∠ABC.
如图,△ABC内接于半圆O,AB为直径,过点A作直线MN,若∠MAC=∠ABC,AE=4,DE=8,求EF
三角形ABC内接于圆O过点A作直线EF AB为直径则我们有角CAE=∠B反过来AB为直径∠CAE=∠B那么EF是圆O的切
如图,三角形ABC内接于圆O,过点B作直线EF,AB为直径,要使得EF是⊙O的切线,需要什么条件(3种)
如图,三角形ABC内接于圆O,过点B作直线EF,AB为直径,要使得EF是⊙O的切线,需要什么条件(3种)
已知三角形内接于圆O,过点A作直线EF,(1)如图1所示,AB为直径,要使EF是圆O的切线,还需要添加的条件是
如图,已知△ABC内接于⊙O,AC是⊙O的直径,D是AB的中点,过点D作直线BC的垂线,分别交CB、CA的延长线E、F.
已知三角形abc内接于圆o,过点a做直线ef.如图二,ab是非直径的弦,角cae等于角b.求证ef是圆o的切线
跟相似性有关:如图,已知O为三角形ABC内一点,过点O作EF平行于BC,GH平行于AB,PQ平行于AC,
(2013•樊城区模拟)如图,已知△ABC内接于⊙O,弦AD交BC于E,过点D的切线MN交直线AB于M,交直线AC于N.
数学题帮下忙哈如图,△ABC内接于⊙O,且∠ABC=∠C,点D在弧BC上运动,过点D作DE‖BC,DE交直线AB于点E,