高一诱导公式(sinA)^2/(sinB)^2+(cosA)^2*(cosC)^2=1,求证：(tanA)^2=(sin

高一诱导公式
(sinA)^2/(sinB)^2+(cosA)^2*(cosC)^2=1,求证：(tanA)^2=(sinc)^2*(tanB)^2

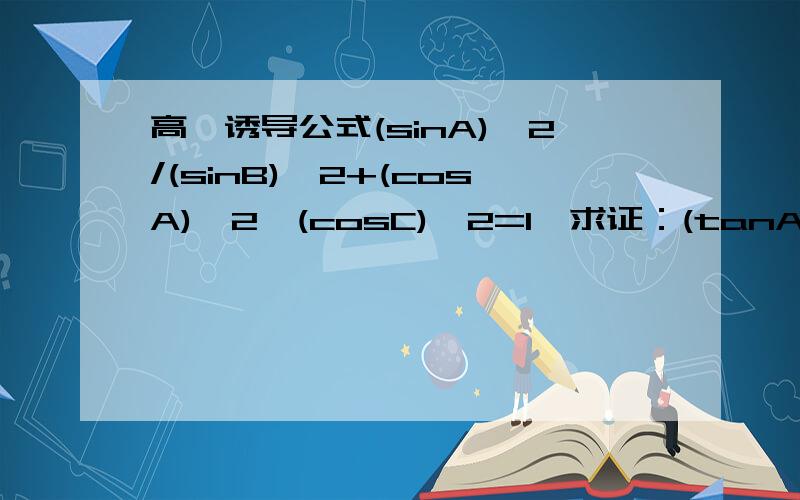
公式一：设α为任意角,终边相同的角的同一三角函数的值相等：弧度制下的角的表示：sin（2kπ＋α）＝sinα （k∈Z） cos（2kπ＋α）＝cosα （k∈Z） tan（2kπ＋α）＝tanα （k∈Z） cot（2kπ＋α）＝cotα （k∈Z） sec（2kπ＋α）＝secα （k∈Z） csc（2kπ＋α）＝cscα （k∈Z） 角度制下的角的表示：sin (α+k·360°)＝sinα（k∈Z） cos(α+k·360°)＝cosα（k∈Z） tan (α+k·360°)＝tanα（k∈Z） cot（α+k·360°）＝cotα （k∈Z） sec（α+k·360°）＝secα （k∈Z） csc（α+k·360°）＝cscα （k∈Z） 公式二：设α为任意角,π+α的三角函数值与α的三角函数值之间的关系：弧度制下的角的表示：sin（π＋α）＝－sinα cos（π＋α）＝－cosα tan（π＋α）＝tanα cot（π＋α）＝cotα sec（π＋α）＝－secα csc（π＋α）＝－cscα 角度制下的角的表示：sin（180°+α）＝－sinα cos（180°+α）＝－cosα tan（180°+α）＝tanα cot（180°+α）＝cotα sec（180°+α）＝－secα csc（180°+α）＝－cscα 公式三：任意角α与 -α的三角函数值之间的关系：sin（－α）＝－sinα cos（－α）＝cosα tan（－α）＝－tanα cot（－α）＝－cotα sec（－α）＝secα csc(－α）＝－cscα 公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：弧度制下的角的表示：sin（π－α）＝sinα cos（π－α）＝－cosα tan（π－α）＝－tanα cot（π－α）＝－cotα sec（π－α）＝－secα csc（π－α）＝cscα 角度制下的角的表示：sin（180°－α）＝sinα cos（180°－α）＝－cosα tan（180°－α）＝－tanα cot（180°－α）＝－cotα sec（180°－α）＝－secα csc（180°－α）＝cscα 公式五：利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系：弧度制下的角的表示：sin（2π－α）＝－sinα cos（2π－α）＝cosα tan（2π－α）＝－tanα cot（2π－α）＝－cotα sec（2π－α）＝secα csc（2π－α）＝－cscα 角度制下的角的表示：sin（360°－α）＝－sinα cos（360°－α）＝cosα tan（360°－α）＝－tanα cot（360°－α）＝－cotα sec（360°－α）＝secα csc（360°－α）＝－cscα 小结：以上五组公式可简记为：函数名不变,符号看象限.即α+k·360°（k∈Z）,－α,180°±α,360°－α的三角函数值,等于α的同名三角函数值,前面加上一个把α看成锐角时原函数值的符号.公式六：π/2±α 及3π/2±α与α的三角函数值之间的关系：（⒈～⒋） ⒈ π/2＋α与α的三角函数值之间的关系 弧度制下的角的表示：sin（π/2＋α）＝cosα cos（π/2＋α）＝—sinα tan（π/2＋α）＝－cotα cot（π/2＋α）＝－tanα sec（π/2＋α）＝－cscα csc（π/2＋α）＝secα 角度制下的角的表示：sin（90°＋α）＝cosα cos（90°＋α）＝－sinα tan（90°＋α）＝－cotα cot（90°＋α）＝－tanα sec（90°＋α）＝－cscα csc（90°＋α）＝secα ⒉ π/2－α与α的三角函数值之间的关系 弧度制下的角的表示：sin（π/2－α）＝cosα cos（π/2－α）＝sinα tan（π/2－α）＝cotα cot（π/2－α）＝tanα sec（π/2－α）＝cscα csc（π/2－α）＝secα 角度制下的角的表示：sin (90°－α)＝cosα cos (90°－α)＝sinα tan (90°－α)＝cotα cot (90°－α)＝tanα sec (90°－α)＝cscα csc (90°－α)＝secα ⒊ 3π/2＋α与α的三角函数值之间的关系 弧度制下的角的表示：sin（3π/2＋α）＝－cosα cos（3π/2＋α）＝sinα tan（3π/2＋α）＝－cotα cot（3π/2＋α）＝－tanα sec（3π/2＋α）＝cscα csc（3π/2＋α）＝－secα 角度制下的角的表示：sin（270°＋α）＝－cosα cos（270°＋α）＝sinα tan（270°＋α）＝－cotα cot（270°＋α）＝－tanα sec（270°＋α）＝cscα csc（270°＋α）＝－secα ⒋ 3π/2－α与α的三角函数值之间的关系 弧度制下的角的表示：sin（3π/2－α）＝－cosα cos（3π/2－α）＝－sinα tan（3π/2－α）＝cotα cot（3π/2－α）＝tanα sec（3π/2－α）＝－cscα csc（3π/2－α）＝－secα 角度制下的角的表示：sin（270°－α）＝－cosα cos（270°－α）＝－sinα tan（270°－α）＝cotα cot（270°－α）＝tanα sec（270°－α）＝－cscα csc（270°－α）＝－secα 温馨提示：1.在做题目的时候,最好将α看成是锐角.2.k∈Z