如图，已知：AB∥CD，求证：∠B+∠D+∠BED=360°．（至少用三种方法）

来源：学生作业帮编辑：大师作文网作业帮分类：数学作业时间：2024/11/19 06:48:42

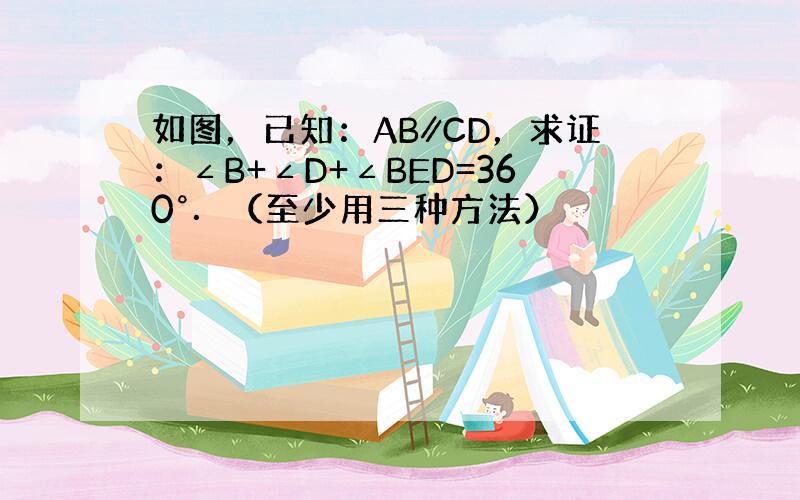
证明：（1）连接BD，如图，
∵AB∥CD（已知），
∴∠ABD+∠CDB=180°（两直线平行，同旁内角互补）．

∵∠1+∠2+∠BED=180°（三角形内角和为180°），
∴∠ABD+∠1+∠CDB+∠2+∠BED=360°，
即∠ABE+∠CDE+∠BED=360°．
（2）延长DE交AB延长线于F，如图
∵AB∥CD（已知），
∴∠F+∠D=180°（两直线平行，同旁内角互补）．

∵∠ABE=∠FEB+∠F，
∠BED=∠FBE+∠F（三角形一个外角等于和它不相邻的两个内角的和）
∴∠ABE+∠CDE+∠BED
=∠FEB+∠F+∠CDE+∠FBE+∠F
=180°+180°
=360°．
（3）过点E作EF∥AB，如图

∵AB∥CD，
∴AB∥EF∥CD（如果两条直线都和第三条直线平行，那么这两条直线也互相平行）
∴∠B+∠BEF=180°
∠D+∠DEF=180°（两直线平行，同旁内角互补）
∴∠B+∠BEF+∠D+∠DEF
=180°+180°
=360°．

已知：AB//CD,求证:∠D+∠B+∠BED=360度（至少用三种方法）已知：如图，∠B+∠BED+∠D=360°．求证：AB∥CD．如图,已知AB∥CD,∠B=58°,∠D=40°,求∠BED的度数.（至少用两种方法求解）. 如图,已知：AB∥CD,求证：∠B＋∠D＋∠BED=360° 如图,已知AB∥CD,求证：∠B=∠D+∠ BED=360度（3种证明）. 如图,已知AB平行CD,那么∠B+∠BED+∠D=360° 如图，已知∠B+∠D=∠BED，试说明AB∥CD．如图,已知∠B+∠D+∠E=360°,求证：AB∥CD 如图，已知AB∥CD，求证：∠B+∠D=∠BED，试完成下列的证明过程．如图,已知∠B+∠D=∠BED,试说明AB∥CD. 如图,已知AB∥CD,试说明∠BED=∠B＋∠D 如图,∠B+∠BED+∠D=360°,试说明AB∥CD.