作业帮 > 数学 > 作业

∫1/sin(3x)dx=?thx

来源：学生作业帮 编辑：大师作文网作业帮 分类：数学作业 时间：2024/11/19 20:55:32
∫1/sin(3x)dx=?thx
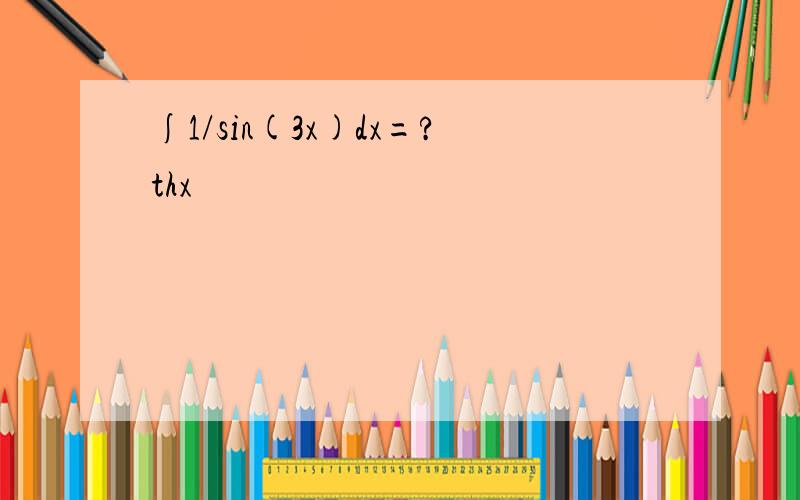
∫1/sin(3x)dx=?thx
∫1/sin(3x)dx
=∫sin(3x)/sin²(3x)dx
=-1/3*∫d[cos(3x)]/[1-cos²(3x)] 令t=cos(3x)则有：
=-1/3*∫dt/(1-t²)
=-1/6*ln|(1+t)/(1-t)|+C 将t=cos(3x)代入有：
=-1/6*ln|(1+cos(3x))/(1-cos(3x))| 进一步化简
=-1/6*ln|(1+cos(3x))²/sin²(3x)|+C
=-1/3*ln|(1+cos(3x))/sin(3x)|+C
∫1/sin(3x)dx=? thx ∫（1-sin^3x）dx ∫sin^3(x)cos^2(x)dx= ∫(3x+1)/[(√4+x²)] dx ∫sin√x dx ∫f(x)dx=ln[sin(3x+1)]+C.求f(x) ∫sin(5x)sin(7x)dx= 求∫√(sin^3x-sin^5x)dx ∫sin²x(1-sin²x)dx是多少? ∫dx/sin^2(2x-3)=? 不定积分：∫dx/(3+sin^2x)= 不定积分∫ sin(5-3x)dx=怎么做 不定积分∫sin(2x+1)dx=?