过双曲线x的平方-y的平方=4上任意一点M作它的一条渐近线的垂线段,垂足为N,0为原点,则三角形OMN的面积为
来源:学生作业帮 编辑:大师作文网作业帮 分类:数学作业 时间:2024/11/18 12:59:24
过双曲线x的平方-y的平方=4上任意一点M作它的一条渐近线的垂线段,垂足为N,0为原点,则三角形OMN的面积为
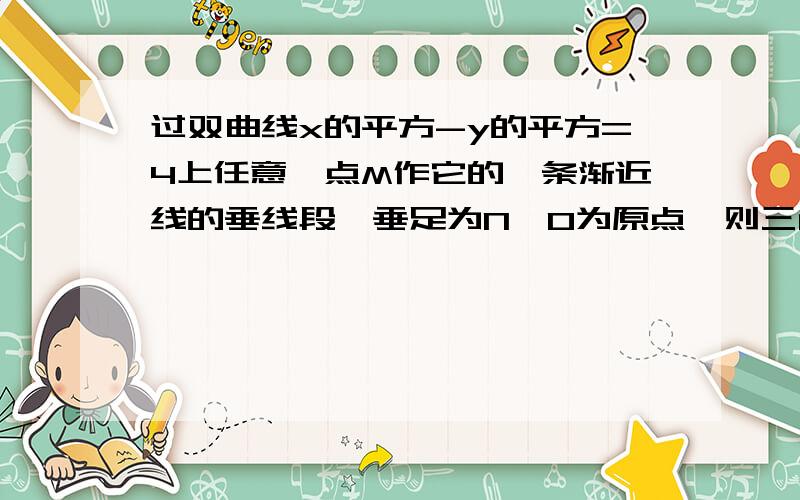
x^2-y^2=4,
——》渐近线的方程为:x^2-y^2=0,即x=+-y,
假设点M在第一象限,坐标为(a,b),点N在渐近线y=x上,则:
MN的方程为:x+y=a+b,
——》xn=yn=(a+b)/2,即N点为((a+b)/2,(a+b)/2),
——》ON=(a+b)√2/2,MN=√[(a-xn)^2+(b-yn)^2]=(a-b)√2/2,
又点M在双曲线上,——》a^2-b^2=4,
——》
S△OMN
=1/2*ON*MN
=1/2*(a+b)√2/2*(a-b)√2/2
=(a^2-b^2)/4
=1.
——》渐近线的方程为:x^2-y^2=0,即x=+-y,
假设点M在第一象限,坐标为(a,b),点N在渐近线y=x上,则:
MN的方程为:x+y=a+b,
——》xn=yn=(a+b)/2,即N点为((a+b)/2,(a+b)/2),
——》ON=(a+b)√2/2,MN=√[(a-xn)^2+(b-yn)^2]=(a-b)√2/2,
又点M在双曲线上,——》a^2-b^2=4,
——》
S△OMN
=1/2*ON*MN
=1/2*(a+b)√2/2*(a-b)√2/2
=(a^2-b^2)/4
=1.
过双曲线x²-y²=4上任意一点M(x0,y0)作它的一条渐近线的垂线垂足为N,O为坐标原点,求△M
过双曲线x平方/a平方—y平方/b平方=1(a>0,b>0)的右焦点F做渐近线y=bx/a的垂线,垂足为M,与双曲线左右
已知双曲线C:x平方/a平方-y平方/b平方=1的左右焦点分别为F1,F2,过F2作双曲线C的一条渐近线的垂线,
已知双曲线x^2/a^2-y^2/b^2=1过右焦点F作一条渐近线的垂线与双曲线交于M垂足为N
已知等轴双曲线C:x^2-y^2=a^2(a>0)的右焦点F,O为坐标原点.过F作一条渐近线的垂线FP且垂足为P,OP长
双曲线与椭圆x平方+2y平方=20有相同的焦点,它的一条渐近线为3x-y=0,则双曲线方程为?
已知双曲线x^2/a^2-y^2/b^2=1 (a,b>0)的右焦点为F,过F作双曲线一条渐近线的垂线,垂足为E,过E作
已知函数求三角形过函数y=6/x图像上一点P作X轴的垂线PQ,Q为垂足,O为坐标原点,则△OPQ的面积为?A 6B 3C
双曲线x平方/4 -y平方/b平方=1的一条渐近线方程为3x-2y=0,则b的值为多少呢?
)过双曲线X^2/A^2 -Y^2/B^2=1(A>B>0)的一个焦点F作一条渐近线的垂线,若垂足恰在OF(O为原点)
过双曲线x2a2−y2b2=1(a>0,b>0)的一个焦点F引它的一条渐近线的垂线FM,垂足为M,并且交y轴于E,若M为
过双曲线x^2/a^2-y^2/b^2=1(a>0,b>0)的右焦点F作渐近线y=b/ax的垂线,垂足为M,与双曲线的左