直角梯形ABCD中,AB平行DC,AB垂直BC,角A等 于60度,AB等于2CD,E、F分别为AB、AD的中 点,连结E
来源:学生作业帮 编辑:大师作文网作业帮 分类:数学作业 时间:2024/11/12 18:51:37
直角梯形ABCD中,AB平行DC,AB垂直BC,角A等 于60度,AB等于2CD,E、F分别为AB、AD的中 点,连结EF、EC、BF、CF.(1)再不添加其他条件下,写出图中一对全等 三角形并予以证明.(2)若CD等于2,求四边形BCFE的面积.
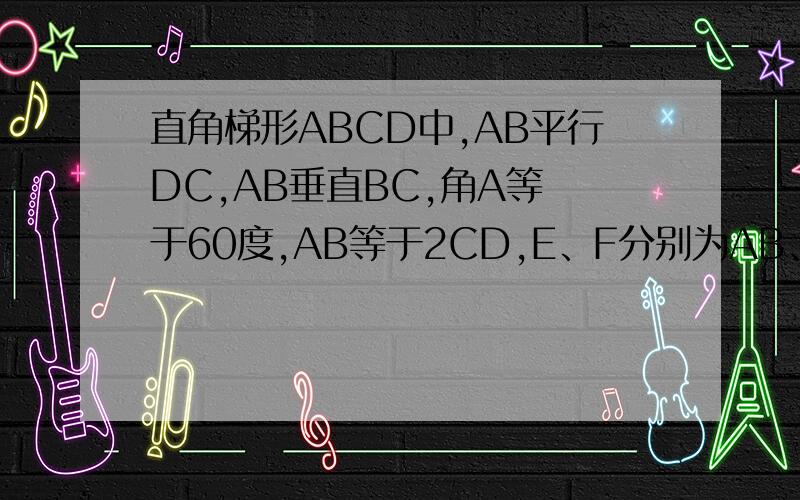
1)△CFE≌△CBE.
证明:因为梯形ABCD中,AB‖DC AB=2CD,E为AB中点.所以AE‖且=CD.所以四边形AECD为平行四边形,所以AD‖且=EC,所以∠CEB=∠A=60°,
因为AB⊥BC,所以∠ABC=90°,所以在RT△BCE中∠CEB=60° CE=2BE
所以AD=CE=2EB,又因为F为AD中点,所以AF=EB=AE,
在三角形AEF中,∠A=60°,AE=AF,所以△AEF为等边三角形,所以AE=AF=EF,∠AEF=60°.所以∠CEF=60°
所以EF=EB
∠CEF=∠CEB
CE=CE
所以△CFE≌△CBE.
(2)因为CD=2、所以BE=2,所以在RT△BCE中,BC=2√3
因为△CFE≌△CBE.所以四边形BCFE的面积=2倍△BCE的面积,所以面积为2*0.5*2*2√3=4√3
证明:因为梯形ABCD中,AB‖DC AB=2CD,E为AB中点.所以AE‖且=CD.所以四边形AECD为平行四边形,所以AD‖且=EC,所以∠CEB=∠A=60°,
因为AB⊥BC,所以∠ABC=90°,所以在RT△BCE中∠CEB=60° CE=2BE
所以AD=CE=2EB,又因为F为AD中点,所以AF=EB=AE,
在三角形AEF中,∠A=60°,AE=AF,所以△AEF为等边三角形,所以AE=AF=EF,∠AEF=60°.所以∠CEF=60°
所以EF=EB
∠CEF=∠CEB
CE=CE
所以△CFE≌△CBE.
(2)因为CD=2、所以BE=2,所以在RT△BCE中,BC=2√3
因为△CFE≌△CBE.所以四边形BCFE的面积=2倍△BCE的面积,所以面积为2*0.5*2*2√3=4√3
在直角梯形ABCD中,AB平行于DC,AB垂直于BC,角A等于60度,AB等于2CD,E F分别为AB AD中点,连接E
在直角梯形ABCD中,AB平行于DC,AB垂直于BC,角A=60度,AB=2CD,E,F分别为AB,AD的重点,连接EF
在直角梯形ABCD中,AB平形CD,AB垂直BC,角A=60度,AB=2CD,E,F分别为AB,AD的中点,连结EF,E
在直角梯形ABCD中,AB平行DC,AB垂直BC,角A=60度,AB=2CD,E.F分别是AB,CD的中点,连接EF,E
在直角梯形abcd中,ab//dc,ab垂直于bc,角a=90°,ab=2cd,e,f分别为ab,ad的中点,连接ef,
如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,∠A=60°,AB=2CD,点E,F分别为AB,AD的中点,连结EF
在梯形ABCD中,AB平行CD,角A等 于90度,AB等于2,BC等于3,CD等于1,E 是AD的
如图 在直角梯形ABCD中,AB‖DC,AB⊥BC,角A=60°,AB=2CD,E、F分别为AB、AD的中点.连接EF、
在梯形ABCD中,AD平行于BC,AB=CD=AD=6,角ABC=60度,点E,F分别在AD,DC上(点E不与点A,D重
在梯形ABCD中,AB平行于CD,点E、F分别是两腰AD、BC的中点.证明:EF平行于AB平行于DC;EF=1/2(AB
已知:在梯形ABCD中,AB平行DC,点E.F分别是两腰AD,BC的中点,证明:EF平行AB平行DC,EF=1/2(AB
如图,在梯形ABCD中,AB平行CD,AD等于DC等于CB,CE垂直AD交AD的延长线于点E,CF垂直AB,垂足为F.(