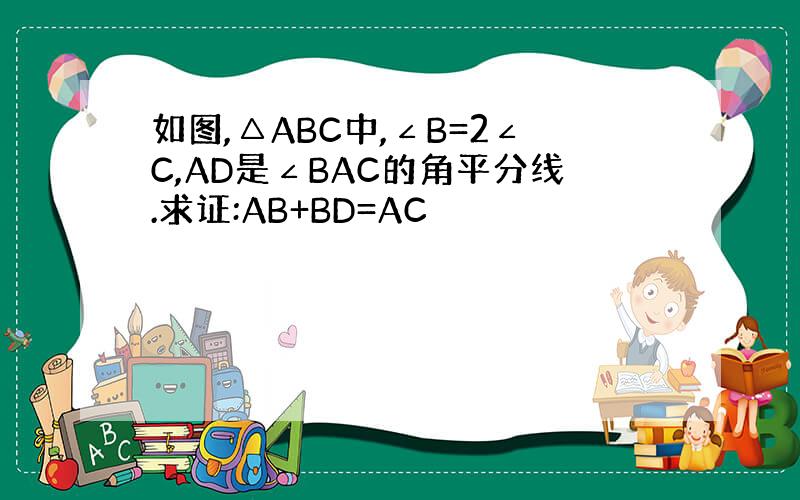
如图,△ABC中,∠B=2∠C,AD是∠BAC的角平分线.求证:AB+BD=AC
如图,在△ABC中,∠B=2∠C,AD为∠BAC的平分线. 求证:AC=AB+BD
如图,在△ABC中,AD是∠BAC的平分线,求证:BD:DC=AB:AC
已知如图,△ABC中,AD是∠BAC的平分线,求证:BD:DC=AB:AC.
如图,在三角形ABC中,角B=2角C,AD是角BAC的平分线,求证:AB+BD=AC
如图,在三角形ABC中,角B=2角C,AD是角BAC的平分线,求证:AB+BD=AC,用补短法.
如图,在三角形abc中 AD是角BAC的平分线 AC=AB+BD 求证:角B=2角C
如图,在△ABC中,AD是∠BAC的平分线,∠C=2∠B,求证:AB=AC+CD
如图,已知在△ABC中,∠B=2∠C,∠BAC的角平分线交BC于D,求证AB+BD=AC
如图,△ABC中,∠B=2∠C,AD是∠CAB的平分线,求证:AC=AB+BD
一道数学证明题 在三角形ABC中,∠B=2∠C,AD是∠BAC的平分线,求证:AC=AB+BD
在Rt△ABC中,∠C=90°,BC=2AC,AD是∠BAC的平分线,求证:AB+2BD=5 AC
如图,在三角形ABC中,AD是角BAC平分线,角B=2陪角C.求证:AB+BD=AC(辅助线)