作业帮 > 综合 > 作业

（2014?长春模拟）如图，在四棱柱ABCD-A1B1C1D1中，底面ABCD和侧面BCC1B1都是矩形，E是CD的中点

来源：学生作业帮 编辑：大师作文网作业帮 分类：综合作业 时间：2024/11/20 06:54:46
（2014?长春模拟）如图，在四棱柱ABCD-A1B1C1D1中，底面ABCD和侧面BCC1B1都是矩形，E是CD的中点，D1E⊥CD
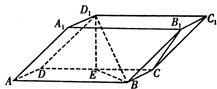（2014?长春模拟）如图，在四棱柱ABCD-A1B1C1D1中，底面ABCD和侧面BCC1B1都是矩形，E是CD的中点，D1E⊥CD，AB=2BC=2．
（1）求证：BC⊥D1E；
（2）若AA1=
2
（2014?长春模拟）如图，在四棱柱ABCD-A1B1C1D1中，底面ABCD和侧面BCC1B1都是矩形，E是CD的中点
（1）证明：∵底面ABCD和侧面BCC1B1是矩形，
∴BC⊥CD，BC⊥CC1，
又∵CD∩CC1=C，
∴BC⊥平面DCC1D1，
∵D1E?平面DCC1D1，∴BC⊥D1E．
（2）在四棱柱ABCD-A1B1C1D1中，DD1∥B1BCC1，
∴三棱锥D1-B1CB的体积等于三棱锥D-B1CB的体积，
就是三棱锥B1-DCB的体积，B1到底面DCB的距离就是D1E，
在四棱柱ABCD-A1B1C1D1中，底面ABCD和侧面BCC1B1都是矩形，E是CD的中点，
D1E⊥CD，AB=2BC=2．
AA1=
2，
∴D1E=
DD12?DE2=
2?1=1．
所求体积：V=
1
3S△DCB?D1E=
1
3×
1
2×2×2×1=
2
3
（2014•潍坊模拟）如图，在四棱柱ABCD-A1B1C1D1中，底面ABCD和侧面BCC1B1都是矩形，E是CD的中点 （平面与平面性质）如图,四棱柱ABCD-A1B1C1D1中底面ABCD为正方形侧棱AA1⊥底面ABCD,E是棱BC的中点 如图，在四棱柱ABCD-A1B1C1D1中，底面ABCD是正方形，侧棱与底面垂直，E，F分别是AB1，BC1的中点，则以 在四棱柱ABCD-A1B1C1D1中,侧面都是矩形,底面都是矩形,底面四边形ABCD是菱形且AB=BC=2√3,∠ABC （2012•湛江模拟）底面是正方形的四棱柱ABCD-A1B1C1D1中，侧棱AA1⊥底面ABCD，E是CC1的中点，O是 如图，四棱柱ABCD-A1B1C1D1中，底面ABCD是正方形，侧棱A1A⊥底面ABCD，E为A1A的中点． 22、如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且垂直于底面,又底面ABCD是矩形,E是侧棱PD的中点. 在四棱柱ABCD-A1B1C1D1中,侧面都是矩形,底面四边形ABCD是菱形且AB=BC=2根号3 （2011•东城区模拟）如图，在四棱柱ABCD-A1B1C1D1中，底面ABCD是正方形，侧棱与底面垂直，点O是正方形A （2014•烟台三模）如图，直四棱柱ABCD-A1B1C1D1中，底面ABCD是菱形，且∠ABC=60°，E为棱CD的中 如图，在正四棱柱ABCD-A1B1C1D1中，E、F分别是AB1、BC1的中点，则以下结论中不成立的是（　　） 如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E,F分别是棱BC,CC1的中点,P是侧面BCC1B1内一点,若