在等腰梯形ABCD中,AB∥BC,△COD是等边三角形,E、F、G分别为OD、OA、BC的中点.求证:△EFG为等边三角
来源:学生作业帮 编辑:大师作文网作业帮 分类:数学作业 时间:2024/11/19 04:51:15
在等腰梯形ABCD中,AB∥BC,△COD是等边三角形,E、F、G分别为OD、OA、BC的中点.求证:△EFG为等边三角形
求证:(1)△AOB为等边三角形.(2)△EFG为等边三角形
求证:(1)△AOB为等边三角形.(2)△EFG为等边三角形

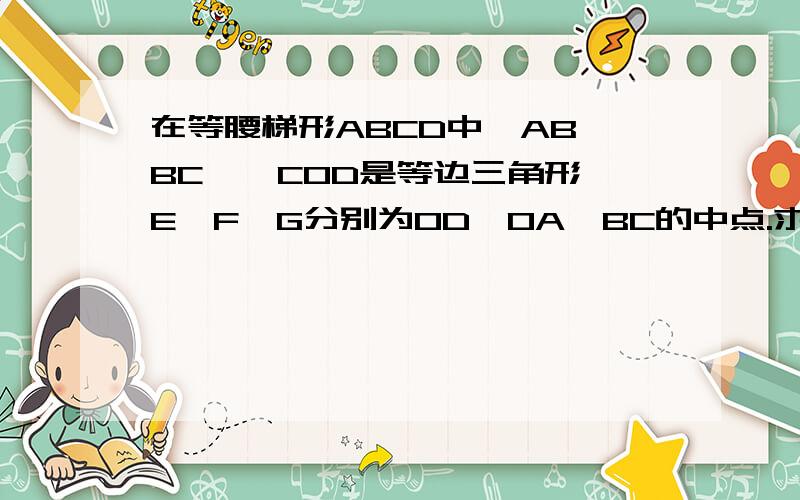
【AB//DC】
证明:
(1)
∵△COD是等边三角形
∴∠OCD=∠ODC=60°
∵AB//DC
∴∠OAB=∠OCD=60°
∠OBA=∠ODC=60°
∴△OAB是等边三角形(有两个角是60°的三角形是等边三角形)
(2)
连接BF,CE
∵E是OD的中点
∴CE⊥OD(等腰三角形三线合一)
∵G是BC的中点
∴EG=½BC(直角三角形斜边中线等于斜边的一半)
同理:BF⊥AO
∴FG=½BC
∵E是OD的中点,F是OA的中点
∴EF是△OAD的中位线
∴EF=½AD
∵四边形ABCD是等腰梯形
∴AD=BC
∴EF=EG=FG
∴△EFG是等边三角形
证明:
(1)
∵△COD是等边三角形
∴∠OCD=∠ODC=60°
∵AB//DC
∴∠OAB=∠OCD=60°
∠OBA=∠ODC=60°
∴△OAB是等边三角形(有两个角是60°的三角形是等边三角形)
(2)
连接BF,CE
∵E是OD的中点
∴CE⊥OD(等腰三角形三线合一)
∵G是BC的中点
∴EG=½BC(直角三角形斜边中线等于斜边的一半)
同理:BF⊥AO
∴FG=½BC
∵E是OD的中点,F是OA的中点
∴EF是△OAD的中位线
∴EF=½AD
∵四边形ABCD是等腰梯形
∴AD=BC
∴EF=EG=FG
∴△EFG是等边三角形
在等腰梯形ABCD中,AD‖BC,AB=DC,E,F,G.H,分别为AD,BE,BC,CE的中点.求证:四边形EFGH
如图,在等腰梯形ABCD中,AB平行DC,AB=DC,E,F,G,H分别为AD,BE,BC.CE的中点.求证:四边形EF
四面体ABCD中,AB=BC,E,F,G分别是AB,BC,CD的中点,且△EFG为正三角形,AG⊥平面BCD
已知:如图,△ABC中,AB、BC、CA的中点分别是E、F、G,AD为BC边上的高,求证:∠EDG=∠EFG
2、已知:在四边形ABCD中,AD=BC,E,F,G,分别是BD,AB,DC的中点 求证:△EFG是等腰三角形
已知:在四边形ABCD中,AD=BC,E,F,G,分别是BD,AB,DC的中点 求证:△EFG是等腰三角形
如图所示,在四边形ABCD中,AD=BC,E,F,G分别是AB,CD,AC的中点.求证:△EFG是等腰三角形.
数字证明题.已知在四面体ABCD中,AC=BD,而且E,F,G,H分别为棱AB,BC,CD,DA的中点,求证四边形EFG
在正方体ABCD——A1B1C1D1中,E,F,G,分别是 AB,BC,AA1,中点.求证B1D垂直面EFG.
初二数学在等腰梯形中ABCD中,AD//BC,MN分别为AB,BC的中点,E,F分别是BM,CM的中点
在梯形ABCD中,AD//BC,点E,F,G,H分别是AD,AB,BC,CD的中点,连接EF,FG,GH,HE.若EFG
如图,在四边形ABCD中,AB=CD,E、F、G分别是BD、AC、BC中点,求证:△EFG是等腰三角形