在矩形abcd中,ae⊥bd于e.若be:ed=1:3,ab=1,求ad
来源:学生作业帮 编辑:大师作文网作业帮 分类:数学作业 时间:2024/11/11 01:43:18
在矩形abcd中,ae⊥bd于e.若be:ed=1:3,ab=1,求ad
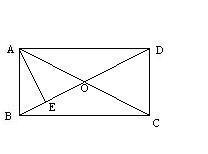


在矩形abcd中,ae⊥bd于e
角aed=角bea并且角ead=角eda
所以△abe相似于△dae
所以be:ae=ab:da
be:ed=1:3,ab=1
所以1:3=1:ad
所以ad=3
再问: 但答案上写的是√3啊
再答: 我写错了 应该是△abe相似于△dae be:ae=ae:be=ab:da 所以be*be=ae*ae be:ed=1:3 ae*ae=be*3be 所以ae=√3be 所以ab:da=be:ae=1:√3 ab=1 所以ad=√3
再问: 你用的是什么方法,咱初二啊
再答: 相似三角形的边长之比相等
角aed=角bea并且角ead=角eda
所以△abe相似于△dae
所以be:ae=ab:da
be:ed=1:3,ab=1
所以1:3=1:ad
所以ad=3
再问: 但答案上写的是√3啊
再答: 我写错了 应该是△abe相似于△dae be:ae=ae:be=ab:da 所以be*be=ae*ae be:ed=1:3 ae*ae=be*3be 所以ae=√3be 所以ab:da=be:ae=1:√3 ab=1 所以ad=√3
再问: 你用的是什么方法,咱初二啊
再答: 相似三角形的边长之比相等
已知;如图在矩形ABCD中,AE垂直BD于点E,若BE:ED=1:3,AB=1,求AD ( 用矩形定理证明)
在矩形ABCD中,AE⊥BD于E,AC,BD相交于O,且BE:ED=1:3,AD=6,求AE的长
已知,如图所示,在矩形ABCD中,AE⊥BD于点E,对角线AC、BD相交于点O,且BE:ED=1:3,若AD=6cm,求
已知如图,在矩形ABCD中,AE⊥BD于E,对角线AC,BD相交于点O,且BE:ED=1:3,AD=6cm,求AE的的长
在矩形ABCD中,AE⊥BD于E.对角线AC,BD交于点O,且BE:ED=1:3,AD=6cm,求AE的长
如图,在矩形ABCD中,AE垂直于BD于点E,对角线AC,BD交于点O,且BE:ED=1:3,AD=6cm,求AE的长
如图,在矩形ABCD中,AE⊥BD于E,对角线AC、DB相较于点O,且BE:ED=1:3,AD=6cm,求AE的长.
如图,在矩形ABCD中,AE⊥BD于E,BE:ED=1:3,AB=4cm,则AC=______.
如图,在矩形ABCD中,AE⊥BD于E,且BE:ED=1:3,求证:AC=2AB.
如图所示,在矩形ABCD中,AE⊥BD于E,对角线AC.BD相交于O,且BE∶ED=1∶3,AD=6㎝,求AE的长.
已知:如图,在矩形ABCD中,AE垂直BD于E,对角线AC.BD交于点O,且BE:ED=1:3,AB=6cm,求AC的长
如图,在矩形ABCD中,AE垂直BD,垂足为E,若BE :ED =1:3,O到AD的距离是m,则角EAD