f (x) =x^2 +kx +4 的最小值为2 ,则k =
来源:学生作业帮 编辑:大师作文网作业帮 分类:数学作业 时间:2024/11/18 21:58:55
f (x) =x^2 +kx +4 的最小值为2 ,则k =
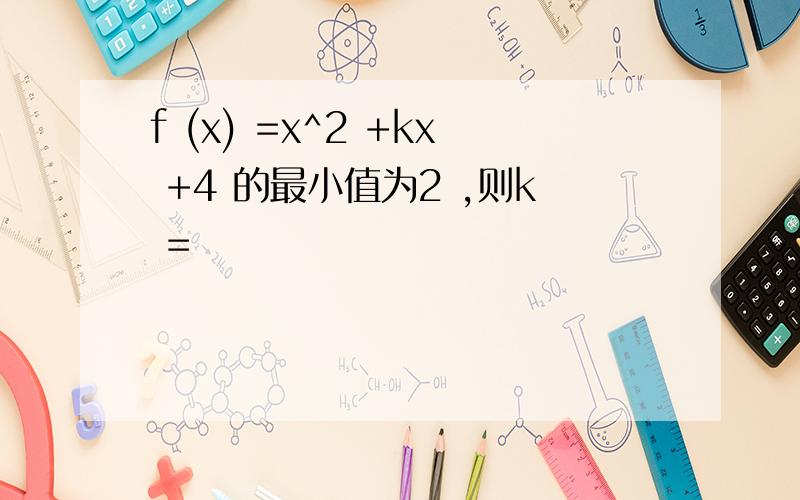
f (x) =x^2 +kx +4
=(x+k/2)²+4-k²/4最小值为2
4-k²/4=2
k²=8
k=±2√2
再问: 下列各式结果是正值的是: A.cos2 B. sin300° C. tan660° D.cot (-150°) 这个怎么分析啊
再答: 结果是正值的是:D.cot (-150°) (-150°为第三象限角,余切为正) A.cos2 (二象限角) B. sin300°(三象限角) C. tan660°(四象限角)
再问: 为什么我不能向你求助
=(x+k/2)²+4-k²/4最小值为2
4-k²/4=2
k²=8
k=±2√2
再问: 下列各式结果是正值的是: A.cos2 B. sin300° C. tan660° D.cot (-150°) 这个怎么分析啊
再答: 结果是正值的是:D.cot (-150°) (-150°为第三象限角,余切为正) A.cos2 (二象限角) B. sin300°(三象限角) C. tan660°(四象限角)
再问: 为什么我不能向你求助
若函数f(x)=x²+kx+4的最小值为2,则k=
函数f(x)=x平方-2kx+k在区间【0,1】上的最小值是1/4则k的值为
已知函数f(x)=x2+kx+1 / x 2+1 若当x>0时,f(x)的最小值为-1,求实数k的值
若函数f(x)=x^2-kx-k=1,在[0,2]上的最小值为g(k),求g(k)的表达式.
函数f(x)=x平方-2kx+k在区间【0,1】上的最小值是1/4,则k等于多少
已知函数f(x)=(2x-3)/(kx^2+4kx+5)的定义域为R,求k范围.
已知函数f(x)=x²-2kx+k+1,若函数f(x)在区间[1,2]上有最小值-5,求实数k的值
k为怎样的值时,函数f(x)=(kx²+4x+k+2)^1\2+(x²-kx+1)°的定义域是R
已知函数f(x)=4x²-kx-8 ,若y=f(x)在区间(-∞,2]上有最小值为-12,求实数k的值
若函数f(x)=(kx+5)/kx^2+4kx+3的定义域为R,则k的取值范围
已知函数f(x)=x^2+kx+1/x^2+1 若当x大于0时,f(x)的最小值为-1,求实数k的值
已知函数f(x)=2cos(kx+π/3)+b(k>0)的最小正周期为π,最小值为3