已知a、b是正实数则 ①√ab＞2ab/a+b ②a＞|a-b|-b ③a^2+b^2＞4ab-3b^2 ④ab+2/a

来源：学生作业帮编辑：大师作文网作业帮分类：数学作业时间：2024/11/13 06:47:33

已知a、b是正实数则 ①√ab＞2ab/a+b ②a＞|a-b|-b ③a^2+b^2＞4ab-3b^2 ④ab+2/ab＞2
呵呵在加一个题哈
a^2+b^2=1,b^2+c^2=2,c^2+a^2=2,求ab+bc+ac的最小值
∵b^2+c^2=2,c^2+a^2=2 ∴a^2+b^2+2c^2=4,
在把a^2+b^2=1代入解得a=±√2/2 b=±√2/2
c=±√6/2
本人觉得只要ab,bc,ca 每个的乘积都为负数就应该是最小值了结果为-1/2-√3 我怎么在网上看到有人等于
1/2-√3

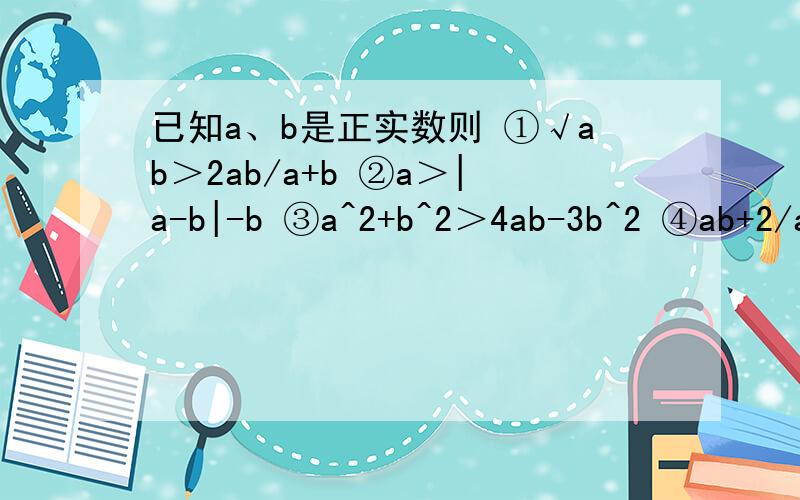
①因a、b是正实数,所以当a≠b时,(√a-√b)^2＞0
a+b>2√ab→(a+b)√ab>2ab→√ab＞2ab/a+b
说明:没有条件a≠b时,应是①√ab≥2ab/a+b,题抄错没有
②因a、b是正实数,所以a+b=│a+b│>│a-b│
所以a+b>|a-b|
即a＞|a-b|-b
③因a、b是正实数,而(a-2b)^2≥0
所以a^2-4ab+4b^2≥0
a^2+b^2≥4ab-3b^2
说明:情况同①,当a≠2b时,才取">"号.
④因a、b是正实数,而(ab-1)^2+1>0
所以(ab)^2-2ab+2>0
(ab)^2+2>2ab
所以ab+2/ab>2

a+b/2ab 2AB/A+B 已知a^2+ab+b^2|ab(a+b),求证(a-b)^3>3ab 已知a.b是正实数,那么,a+b/2≥根号ab是恒立的已知a,b是正实数,求ab/(a^2+a+1)(b^+b+1)的值已知实数a,b满足ab=-1/5,a+b=4/5,求a^2b+ab^2-a^3b^2-a^2b^3 已知a,b为实数,则a²+ab+b²-a-2b的最小值已知a+b＞0,求证a^3-a^2b大于ab^2-b^3 （a-b)(a^2+ab+b) 化简一道很有挑战性的题目已知a,b是不相等的正实数,求证：【（a^2)b+a+b^2】(ab^2+a^2+b)＞(3ab)^ 已知实数a,b满足√a/b(√ab+2b)=2√ab+3b,则a/b 已知a,b,c是实数,求证a*a+b*b+c*c>=ab+3b+2c