(x y)dx (y-x)dy=0
来源:学生作业帮助网 编辑:作业帮 时间:2024/11/13 06:58:45
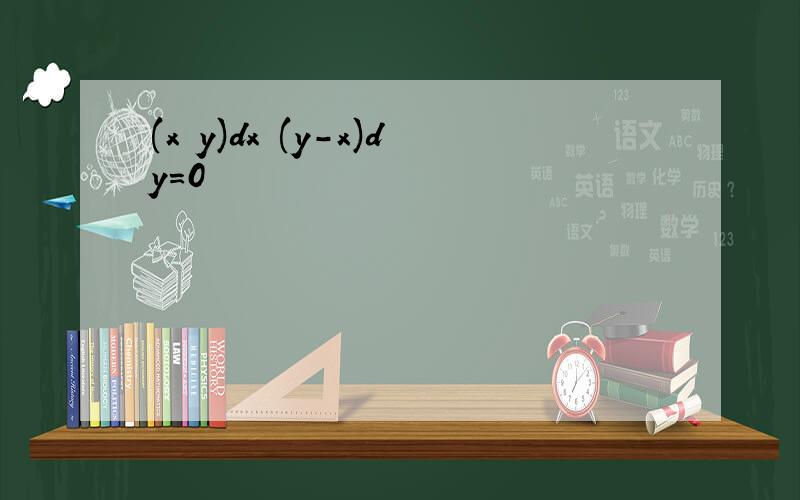
(1+x*x)=C(1+y*y)
y(x^2-xy+y^2)dx+x(x^2-xy+y^2)dy=0(x^2-xy+y^2)(dxy+dxy)=0(x^2-xy+y^2)*2dxy=02dxy=0(1)或者x^2-xy+y^2=0(2
解析2xdx+ydx+xdy+3y²dy=0(2x+y)dx+(x+3y²)dy=0(2x+y)dx=-(x+3y²)dydy/dx=(2x+y)/-(x+3y²
x^2*dy/dx=xy-y^2dy/dx=y/x-y^2/x^2u=y/xy=xuy'=u+xu'代入:u+xu'=u+u^2xu'=u^2du/u^2=dx/x-1/u=lnx+lnCCx=e^(
方法一(微分法)d(y/x)=d(ln(xy))(xdy-ydx)/x²=1/xy*d(xy)即(xdy-ydx)/x²=(ydx+xdy)/xy∴dy/dx=(xy+y²
(xy^2-x)dx+(x^2y+y)dy=0xy^2dx-xdx+x^2ydy+ydy=0xy^2dx+x^2ydy-xdx+ydy=02xy^2dx+2x^2ydy-2xdx+2ydy=0注意:d
令u=y/x,怎样推到dy/dx=u+x*du/dx令u=y/x,y=x*u,y'=u+x*u'即dy/dx=u+x*du/dx
两边求导(y'x-y)/x^2=(y+xy')/xyxy+x^2y'=xyy'+y^2y'=(xy-y^2)/(xy+x^2)
(xy^2+x)dx+(y-x^2y)dy=0dx^2y^2+dx^2+dy^2-dx^2y^2=0d(x^2+y^2)=0x^2+y^2=0x=0y=0同学,遇到问题自己先考虑
令z=1/x,则dx=-x²dz代入原方程得(x²y³+xy)dy=-x²dz==>dz/dy+y/x=-y³==>dz/dy+yz=-y³
e^(x+y)-xy=1两边同时求导,e^(x+y)*(1+dy/dx)-y-xdy/dz=0(1)验证x=0,y=0在原曲线上.令x=0,y=0代入到(1)e^0*(1+dy/dz)-0-0*dy/
原式变形有y[(2xy-1)dx+(x+y)dy]=0当y=0时显然成立.当(2xy-1)dx+(x+y)dy=0,这不是一个齐次方程,显然就不是一个恰当方程,无解.我们不妨反证一下此方程无如果存在d
your answer here
∵(2x+xy^2)dx+(2y+x^2*y)dy=0==>(xy^2dx+x^2*ydy)+(2xdx+2ydy)=0==>d(x^2*y^2)+2d(x^2+y^2)=0==>x^2*y^2+2(
别人一般问一道题,你一下子5道?我给你个提示:1.所有5道题全部可以化成y'=f(y/x)的形式.比如5::y’=√(1-y^2/x^2)+y/x2.设y/x=uy=xuy'=u+xu',代入:u+x
做边量替换,u=y/x,即y=uxy’=u+xu'原方程左右同除x^2y变为(1-u+u^2)+(1/u+1+u)(u+xu')=0积分再换回变量就是答案了不知道你会不会积分,再问:还是写下过程吧,没
dy/dx=x(y²+1)/(y-xy²)
是xy-[1/(x^2y)]dx-[1/(xy^2)]dy=0还是[(xy-1)/(x^2y)]dx-[1/(xy^2)]dy=0请表达清楚,无歧义!再问:[(xy-1)/(x^2y)]dx-[1/(
两边同时求导x+x(dy/dx)+1*(dy/dx)/y+1/x=0合并同类项dy/dx=-y/x