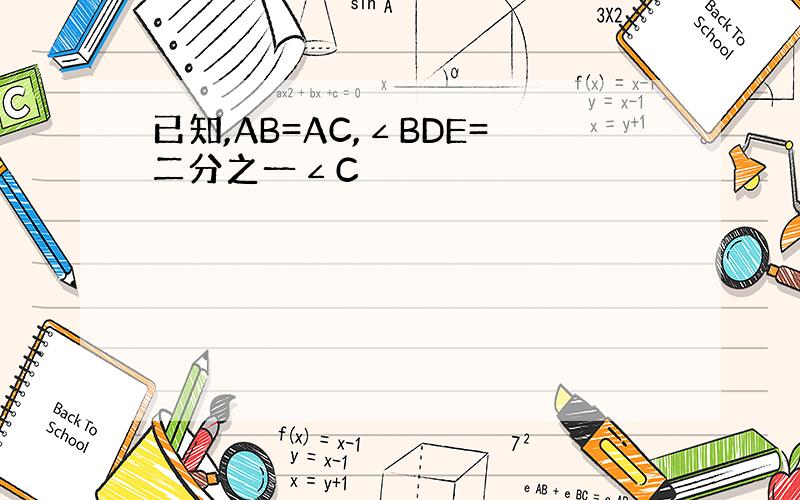
已知,AB=AC,∠BDE=二分之一∠C

因为CD=CE,所以角CDE=角CED,因为AC=BC,所以角A=角B,由题,有角CDE=角A+40度-角BDE=角CED=角B+角BDE,即角A+40度=角B+2角BDE,所以角BDE为20度

70再答：再答：

AD平分∠BAC,AE=AC,则△ADE和△ADC全等,则DE=DC,又AC=AE=15cm,所以周长=AC+AB+BC=AC+(AE+EB)+(BD+DC)=AC+(AC+EB)+(BD+DE)=2

1.易知三角形ABC与三角形BDE为全等三角形,那么连接CM,ME,EN.因三角形全等,可知NE=CM.又由于N点位中点,AB=2BC=BD所以CN=ME所以四边形CNEM两两对边相等,所以四边形CN

证明：（1）∵∠BDE=∠CDE，∴180°-∠BDE=180°-∠CDE，即：∠ADB=∠ADC．∵AE为角平分线，∴∠BAD=∠CAD．又∵AD=AD，∴△ADB≌△ADC（ASA）∴AB=AC．

设O是ABCD中心,CE＝EF＝CO＝1,EF‖＝CO,∴ACEF是菱形.CF⊥AE,DB⊥AC∴DB⊥ACEF（∵ADEF⊥ABCD）∴CF⊥BD,得到CF⊥平面BDE

证明：∵∠1=180-（∠B+∠BED）∠2=180-（∠DEF+∠BED）∠B=∠DEF∴∠1=∠2∵BD=CE∴△BDE和△CEF是全等三角形

因为B.D.E在同一直线上所以∠BDE=180°

三角形的外角等于两内角之和,有：∠BDE=∠BAD+∠ABD,∠CDE=∠CAD+∠ACD （1）AE为角平分线,D为AE上一点,有：∠BAD=∠CAD   &

三角形BDE全等于三角形CEF因为AB=AC所以角B=角C因为角B+角BDE+角DEB=180角DEF+角CEF+角DEB=180且角B=角DEF所以角BDE=角CEF又因为BD=CE所以这两个三角形

平行,做一条平行于AB,并且过点E,然后根据内错角相等就可以了

∵DE平分∠ADC、∠ADC=90°∴∠ADE=∠EDC=45°∴∠BDE=15°∴∠ADB=30°∴BD=8、BC=AD=4√3、EC=DC=AB=4∴BE=BC-EC=4√3-4设E到BD的距离为

分别连接BE、BC,∵AB=AC,∠BAC=120°,∴∠ABC=30°,∵DB=DE,∠BDE=120°,∴∠DBE=30°,∴∠ABC=∠DBE=30°,∴ΔABC∽ΔGBE,∴BC/BE=AB/

∵∠CDB为△ACD的外角∴∠CDB=∠A+∠ACD=∠A+40°又∵AC=BC∴∠B=∠A∴∠CDB=∠B+40°又∵CD=CE∴∠CDE=∠CED又∵∠CDB=∠CDE+∠EDB=∠CED+∠ED

要用到四点共圆了

连接ED,延长ED,CA交于点F,连接BF因为AD垂直平面ABC,EC垂直平面ABC所以AD//EC因为CE=2AD所以AD是三角形FCE的中位线所以AF=AC因为AB=AC所以AB=AF=AC所以角

方法一：延长ED交CA的延长线于F.∵AD⊥平面ABC、CE⊥平面ABC,∴AD∥CE,又CE＝2AD,∴AC＝AF,又AB＝AC,∴AB＝AC＝AF,∴A是△BCF的外心,∴BF⊥BC.∵CE⊥平面

∵∠BDE=∠ABC+∠BAD，∴∠ABC=∠BDE-∠BAD=100°-70°=30°，∵AB=AC，∴∠ABC=∠C=30°，∴∠BAC=180°-∠ABC-∠C=120°，∴∠CAD=∠BAC-

∵AB=AC，AD是高∴∠BAD=∠CAD=26°∵∠AD=AE∴∠ADE=∠AED=（180°-26°）÷2=77°∵AD是高∴∠BDE=90°-77°=13°．

其实这个题你如果知道一个结论可秒角平分线定理2：三角形一个角的平分线,这个角平分线其对边所成的两条线段与这个角的两邻边对应成比例举个例子三角形ABC,AD角平分线则AB/AC=BD/DC证明无论是面积