BC ⊥∥1 2FG,
来源:学生作业帮助网 编辑:作业帮 时间:2024/11/06 14:43:15
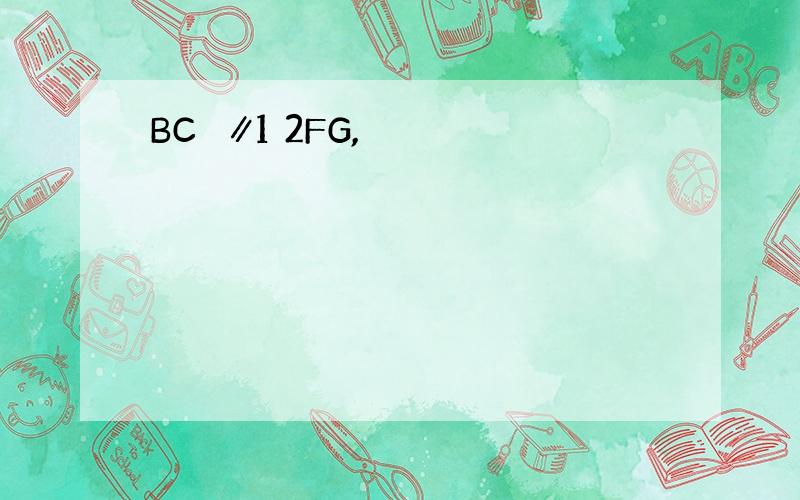
∵AE⊥BC∴∠EMB=90°∵FG⊥BC∴∠FNB=90°∴∠EMB=∠FNB∴AE∥FG∴∠EAB=∠1∵∠1=∠2∴∠EAB=∠2∴AB∥CD
证明:(Ⅰ)∵EF∥AB,FG∥BC,EG∥AC,∠ACB=90°,∴∠EGF=90°,△ABC~△EFG,由于AB=2EF,∴BC=2FG,连接AF,∵FG∥BC,FG=1/2BC,在▱
证明:∵AD⊥AB,AD⊥AC,∴AD⊥平面ABC∴AD⊥BC∵AE⊥BC∴BC⊥平面ADE在△AFG中,D是FG的中点,AF=AG,得AD⊥FG在△EFG中,D是FG的中点,EF=EG,得ED⊥FG
过点E作EH⊥BC于H,∵CE平分∠ACB,EH⊥BC,EA⊥AC∴AE=EH∵∠AEF+∠ACE=90°,∠CFD+∠DCF=90°∠DCF=∠ACF∴∠AEF=∠CFD∵∠AFE=∠CFD∴∠AE
角AEC=90º-ACE=90º-BCE=CGD=AGE,所以AE=AG.(1)FG//BC,所以BF/DG=AF/AG.(2)过F做直线垂直BC于H,则∆BFH和&#
连接OB,延长OF,OE分别交BC于H,交AB于G,∵DE、FG分别与⊙O相切于E、F两点,∴OE⊥ED,OF⊥FG,∵AB∥DE,BC∥FG,∴OG⊥AB,OH⊥BC,∵∠EOF=90°,∴四边形B
第一题的G是什么?2延长AC,BE,交于I,延长CF交AB于点H,∵∠1=∠2,AE⊥HC,AE⊥BI∴等腰直角△AHC和ABI,∴AH=AC,AB=AI∴HB=CI.∵F,G,E分别为HC,BC,B
S1:S2:S3=1:3:12则△ADE面积:△AFG:△ABC=1:4:16根据公式,相似三角形面积之比等于边长之比的平方所以DE:FG:BC=1:2:4所以DE=4,FG=8
证明:∵DE∥BC,∴∠1=∠DCB,又∵∠1+∠2=180°,∴∠DCB+∠2=180°,∴CD∥GF,∵CD⊥AB,∴FG⊥AB.
证明:因为:DE//BC所以:∠DEB=∠EBC(直线平行,内错角相等)因为:∠DEB=∠GFC所以:∠DEB=∠EBC=∠GFC(等量替代)所以:BE//FG(同位角相等,直线平行)
证明:∵DE∥BC,∴∠1=∠BCD,又∠1=∠2∴∠2=∠BCD∴FG∥CD又∵CD⊥AB∴FG⊥AB.
因为:FG平行BC所以:∠EFG=∠ECB=∠ACF,∠EGF=∠ABC=∠CAD所以:△ACF∽△GFE所以:∠AEF=∠AFE所以:AF=AE=2因为△ACD∽△ABC所以:CD/AC=AC/BC
图有点不标准..很简单的∠B+∠BAC=90=∠BAC+∠ACE所以∠B=∠ACE又GF//BC,所以∠B=∠AGF=∠ACE又AF=AF,∠GAF=∠CAF根据角角边得AGF全等于ACF所以AG=A
FG⊥AB,∵DE∥BC,∴∠2=∠C(两直线平行,内错角相等).∵∠1=∠2,∴∠1=∠C,∴CD∥FG(同位角相等,两直线平行).又∵CD⊥AB,∴FG⊥AB(若一条直线垂直于两条平行线中的一条,
解题思路:见解答过程解题过程:中国已就“十二五”规划编制前期工作进行部署,该规划将深化对一些全局性、战略性重大问题的研究,就解决经济社会发展的突出矛盾和问题提出相应措施。提出通
连结GD、DF,∵〈BGC=〈BFC=90°,∴△BGC和△BFC都是RT△,∵D是BC的中点,∴GD和DF分别是RT△BGC和RT△BFC斜边上的中线,∴GD=BC/2,DF=BC/2,(RT△斜边
面积比等于边长比的平方,面积比为1:2:3.所以DE:FG:BC=1:√2:√3.DE=4*√3.FG=4√6
再答:过程看图再答:过程我检查过了,绝对正确。我是第一个回答正确答案给你的,求采纳谢谢再答:求采纳谢谢我是第一个回答正确答案给你的,再答:点击右上角采纳我啊我是第一个回答正确答案给你的再问