dy dx-y=2ex

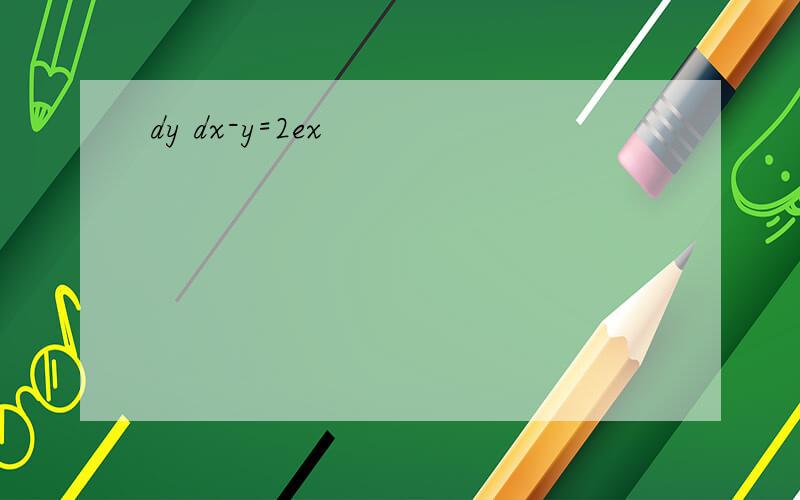
方程两边求关x的导数ddx(xy)＝(y+xdydx)；     ddxex+y＝ex+y(1+dydx)；所以有  （y+xdy

∵微分方程两边除以2，得同解的微分方程y″+12y′−12y＝ex对应的齐次方程为y″+12y′−12y＝0∴特征方程为r2+12r−12＝0，解得特征根为：r1＝−1，r2＝12∴齐次方程的通解为：

特征方程为r^2+1=0,r=±i所以y1=C1sinx+C2cosx设y2=Ae^x则y2''=Ae^x2A=1,A=1/2所以y=y1+y2=C1sinx+C2cosx+e^x/2再问：确定吗？怎

E(X+2Y)^2=E(X^2+4XY+4Y^2)=E(X^2)+4E(XY)+4E(Y^2)=DX+(EX)^2+4EX*EY+4DY+(EY)^2=1+0^2+4*0*0+4*1+0^2=5

方程两边对x求导得2x+y′x2+y＝3x2y+x3y′+cosxy′＝2x−(x2+y)(3x2y+cosx)x5+x3y−1由原方程知，x=0时y=1，代入上式得y′|x＝0＝dydx|x＝0＝1

y=e^x-lncosx,这是函数的和差以及复合函数的综合求导应用.y'=e^x-(1/cosx)*(cosx)'y'=e^x-(1/cosx)(*-sinx)y'=e^x+tanx所以：dy=(e^

微分方程y″-2y′-3y=3x+1+ex的特征方程为：λ2-2λ-3=0，求解可得其特征值为：λ1=-1，λ2=3．对于微分方程y″-2y′-3y=3x+1，①由于0不是方程的特征根，故其特解形式为

y=x³=(x+1)(x²+4)=x³+x²+4x+4x²+4x+4=(x+2)²=0x=-2Thecommonpointis(-2,-8)

(2X+1)/(X+1)

eZ/eX=2x*[ef(x*x-y*y)/ex],eZ/eY=-2x*[ef(x*x-y*y)/ey],

这是一阶线性微分方程，其中P（x）=1，Q（x）=e-x∴通解y＝e−∫dx(∫e−x•e∫dxdx+C)＝e−x(∫e−x•exdx+C)＝e−x(x+C)．

dydx要是等式才行吧.如果是的话,这句话就是求这个等式的根,用r表示x.

e^(x＋2)：表示e的(x＋2)次方y=e^(x＋2)ln(y)=x＋2x=lny－2反函数是：y=(lnx)－2,其中x>0

设切点为（x0，y0），则y0=2ex0，∵y′=（2ex）′=2ex，∴切线斜率k=2ex0，又点（x0，y0）在直线上，代入方程得y0=kx0，即2ex0=2ex0x0，解得x0=1，∴k=2e．

∵点（2，e2）在曲线上，∴切线的斜率k=y′|x•2=ex|x•2=e2，∴切线的方程为y-e2=e2（x-2）．即e2x-y-e2=0．与x轴的交点坐标为（1，0），∴曲线y=ex在点（2，e2）

解题思路：分析：根据导数的几何意义求出切线的斜率，再根据直线方程的点斜式方程求出切线方程。解题过程：

y=x^(e^x)(1)lny=e^xlnx(2)//:对(1)两边取对数y'/y=e^x(lnx+1/x)(3)//:(2)两边对x求导y'=x^(e^x)e^x(lnx+1/x)(4)//:最后结

因为点（x，y）和点（x，-y）关于x轴对称，所以y=-ex的图象与y=ex的图象关于x轴对称，故A和B错误；因为点（x，y）和点（-x，-y）关于原点对称，所以y=-ex的图象与y=e-x的图象关于

=√2/2

在方程ex+y+cos（xy）=0左右两边同时对x求导，得：ex+y（1+y′）-sin（xy）•（y+xy′）=0，化简求得：y′＝dydx＝ysin(xy)−ex+yex+y−xsin(xy)．