lim(x^2 1)(2x 5)^8 (2x-9)^10
来源:学生作业帮助网 编辑:作业帮 时间:2024/11/12 07:59:38
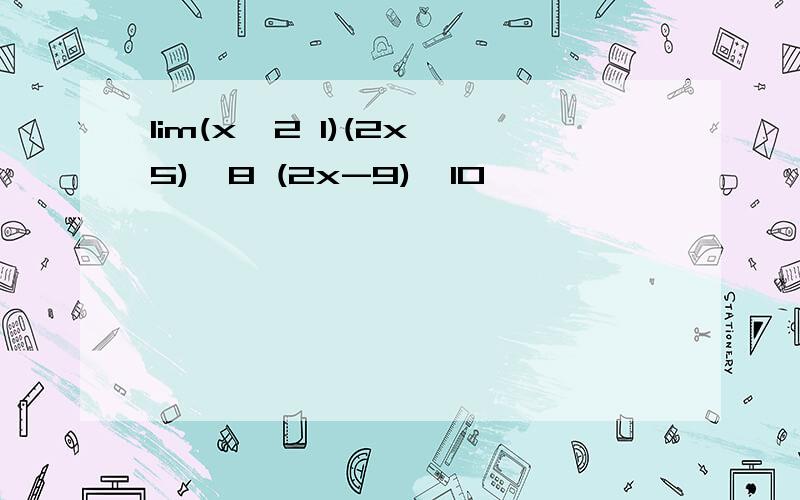
你可以先求这个极限的倒数发现是0那么你可以得到这个就是1/0这个当然是无穷大.再问:答案是这再答:对的对的你提醒了我这类题目要考虑左极限和右极限答案是更加准确的。
我是这样理解的lim(X->0)sin2x/x=lim(X->0)2(sin2x/2x)sin2x/x=2sin2x/2x﹙分子分母同乘以2﹚这就转化为公式lim﹙X->0)sinx/x=1∴为2再问
是x→0吗?属于1^(∞)型,取自然对数,用罗彼塔法则,分子、分母同时求导,原式=lim[x→0]ln(x+e^2x)/sinx=lim[x→0][(1+2e^2x)/(x+e^2x)]/cosx=[
X5+X+1=X5-X4+X4-X3+X3-X2+X2+X+1=X4(X-1)+X3(X-1)+X2(X-1)+X2+X+1=X2(X-1)(X2+X+1)+(X2+X+1)=(X2+X+1)(X3-
您没限制x的取向,所以要分情况;123再问:忘打了。。X➡2+X➡2-单侧极限再答:没有极限,叫无穷;有三种情况:一般,极限,无穷;画出来属于无穷
你这个题目,应该是x→00吧?1-(2/x)=(x-2)/x,它的-1次方就是x/(x-2),当x取无情大的时候,极限取1我的答题到此结束,
1/1X3+1/3X5+1/5X7+.+1/(2x-1)(2x+1)=10/211/2*(1-1/3)+1/2*(1/3-1/5)+1/2*(1/5-1/7)+.+1/2*[1/(2x-1)-1/(2
1-pi*pi(x^2-1)/cosx在点x=pi是连续的,所以代入x=pi就是所求的极限值.
(1)sin2x5xsin2x2lim-------------------=lim--------------*lim------------*------=2/5x→0sin5xx→0sin5xx
120再答:60再问:过程再答:2x+24=1442x=120x=60
答:lim(x→0)(1-cosx)/x²=lim(x→0)2sin²(x/2)/[4*(x/2)²]=lim(t→0)(1/2)(sint/t)²=1/2
-1/8用罗比达法则
sin1/x^2在x->0时没有极限,所以极限不存在.(1^p+2^p+3^p.+n^p)/n^(p+1)可以看作(i/n)^p中i从1到n的求和再求算术平均.可以看作一个函数f(x)=x^p在(0,
1.(2)(x5+2)(x5-1)1.(4)2.(1)(x+2)2(x-1)满难的其他解不出唉
题目不完整.缺x趋向?
1*5+2*5+...+n*5=(1+2+...+n)*5=n(n+1)*5/2
lim(x->0)x/(sinx)^2=lim(x->0){[x/(sinx)]^2}/x=∞这是因为lim(x->0)x/sinx=1
原式=lim(x->0)sinx(secx-1)/x^3=lim(x->0)(secx-1)/x^2=lim(x->0)(1-cosx)/x^2cosx=lim(x->0)2sin^2(x/2)/x^
最简单的解法:利用等价无穷小代换定理,由sinx与x等价,1-cosx与x^2/2等价,则lim(tanx-sinx)/x^3x→0=lim[sinx(1-cosx)]/(cosx·x^3)x→0=l