x1＝√2.xn 1＝√2xn,n＝1,2,.

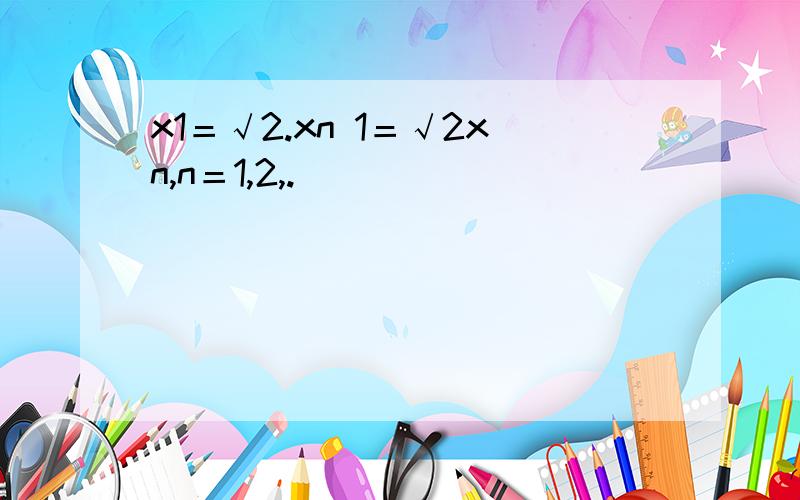
1.你写的①②根本不是命题,何来“证明”一说?既然是证明,你把“已知条件”、“求证”写清楚好不好?2. 请把下标写清楚,   你这样写,鬼知道 你要写

问题一般化：设X1≥0,Xn=√( a+X[n-1]) ﹙n=2,3...),求极限limXn首先,对任意正整数n,xn>0；  其次,x1<x2.

证明：∵X1>0,Xn+1=(1/2)(Xn+a/Xn)(n=1,2...,a>0)==>Xn>0(n=1,2...,)(应用数学归纳法证明)==>Xn+1=(1/2)(Xn+a/Xn)≥(1/2)(

x1x2..xn均为整数应是x1x2..xn均为正数吧,由均值不等式得：(x2/√x1)+√x1≥2√x2,(x3/√x2)+√x2≥2√x3,...(x1/√xn)+√xn≥2√x1,把上面n个不等

a>=0,x1>=0,Xn+1=1/2(Xn+a/Xn)有：xn>=0,Xn+1=1/2(Xn+a/Xn)>=2*1/2*√a=√a即xn>=√a;n>=2xn+1-xn=1/2*(xn+a/xn-2

收敛好证,极限难求啊!点击图片有收敛证明

x2/√x1+√x1≥2√x2x3/√x2+√x2≥2√x3.x1/√xn+√xn≥2√x1全部相加得：（x2/√x1+x3/√x2+……x1/√xn)+√x1+√x2+……√xn)≥2(√x1+√x

若n≤19,∵|xi|＜1(i=1,2,···,n)∴|x1|+|x2|+······+|xn|＜n≤19≤19+|x1+x2+······+xn|,与题中|x1|+|x2|+······+|xn|=

存在正整数ab满足条件的,事实上a=1,b=1时Xn＋2＝Xn＋1＋Xn＋a√（Xn＋1*Xn＋b）即Xn＋2＝Xn＋1＋Xn＋1√（Xn＋1*Xn＋1）Xn＋2＝Xn＋1＋Xn＋1*|（Xn＋1）|

写成指数函数形式,2为底,指数是单增的,等比级数求和,可求极限,利用指数函数连续性,或用归纳法证xn单增且有上界,极限存在,对公式两边Xn+1=√2xn求极限

Xn+1=(√2*Xn)/(√Xn^2+2)Xn+1^2=2*Xn^2/(Xn^2+2)1/X(n+1)^2=(1/2)*(1+2/Xn^2)=1/2+1/Xn^2所以{1/Xn^2}为等差数列,公差

数学归纳法当n=1时,显然成立设n=k时成立则,n=k+1时x(k+1)=(Xn/2)+(1/Xn)(Xn/2)

首先,Xn+1=1/2(Xn+a/Xn)>=1/2*2√a=√a则无论X1>0的值如何（所以可假定X1>√a）,Xn(n=2,3...)的值都大于或等于√a如果X1=√a可以确定,Xn为常数列,其极限

1、当x1=3时,显然该数列xn=3,极限存在；2、当x1>3时,用数学归纳法来证明数列单调有界x2=√(x1+6)>√(3+6)=3假设xk>3,下证x(k+1)>3x(k+1)=√(xk+6)>√

接管时填数字还是表达式?

应用单调有界准则①先证单调性（应用数学归纳法）②再证有界性（应用数学归纳法）所以数列单调递增且有上界,于是数列的极限存在.敬请及时采纳,回到你的提问页,点击我的回答,然后右上角点击“评价”,然后就可以

这个不等式恒成立用柯西不等式便可证明出(x1^2+x2^2+x3^2+.+xn^2)*(1+1+1+.+1)>=(x1+x2+x3+.+xn)^2仅当x1=x2=x3=.=xn,等号成立所以这个不等式

天啊,一看到数学符号我就超级头大.再问：尼玛！你……欠扁吧！再答：不好意思啊，我不是故意的，的确是看见那个有点头大，麻烦你不要说脏话好吗？再问：呵呵！不好意思！O(∩_∩)O再答：嗯，没事的，呵呵

当n>=3时Xn=√(2+Xn-1)=√(2+√(2+Xn-2))>√(2+Xn-2)=Xn-1易证X1

强烈要求加分.这个就是差分方程,关于他的解都有定论Xn+1-根号a=1/2（根号Xn-根号（a/Xn））^2Xn+1+根号a=1/2（根号Xn+根号（a/Xn））^2(Xn+1-根号a)/(Xn+1+