∫ln(1 x)²dx-搜答案-大师作文网

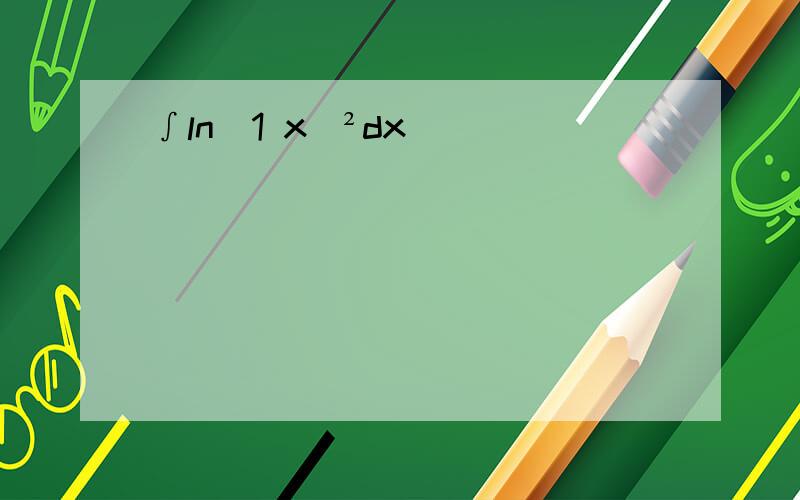
∫ln(1+x^2)dx

∫ln(1+x²)dx=x•ln(1+x²)-∫xdln(1+x²)=xln(1+x²)-∫x•1/(1+x²)•

见图

∫e^x(1/x+lnx)dx=∫e^xdlnx+∫lnxde^x=e^xlnx-∫lnxde^x+∫lnxde^x+C=e^xlnx+C

先将被积函数展开成幂级数,再逐项积分.ln（1-x）=x+x²/2+x³/3+x^4/4+……所以ln（1-x）/x=1+x/2+x²/3+x³/4+……逐项积

∫ln(x+√(1+x^2))dxletx=tanadx=(seca)^2da∫ln(x+√(1+x^2))dx=∫(seca)^2ln(tana+seca))da=∫ln(tana+seca))d(

∫ln(1+x²)dx

∫x*ln(x-1)dx

用分步积分∫x*ln(x-1)dx=1/2∫xln(x-1)dx^2=1/2x^2ln(x-1)-1/2∫x^2dln(x-1)=1/2x^2ln(x-1)-1/2∫x^2/(x-1)dx=1/2x^

原式=∫ln(1-x)d(1-x)=(1-x)ln(1-x)-∫(1-x)dln(1-x)=(1-x)ln(1-x)-∫(1-x)*[-1/(1-x)]dx=(1-x)ln(1-x)+∫dx=(1-x

设u=ln(1+x)-lnx.∫[ln(1+x)-lnx]/x(1+x)dx=-∫udu=-1/2u²+C=-1/2[ln(1+x)-lnx]²+C

∫x* ln (x-1) dx

用分部积分法：∫x*ln(x-1)dx=1/2∫xln(x-1)dx^2=1/2x^2ln(x-1)-1/2∫x^2dln(x-1)=1/2x^2ln(x-1)-1/2∫x^2/(x-1)dx=1/2

∫ln(1+x)/(1+x)dx=∫ln(1+x)/(1+x)d(1+x)=∫ln(1+x)dln(1+x)=[ln(1+x)]²/2+C

用分部积分法,(uv)'=u'v+uv',设u=ln(1+x^2),v'=1,u'=2x/(1+x^2),v=x,原式=xln(1+x^2)-2∫x^2dx/(1+x^2)=xln(1+x^2)-2∫

原式=∫(1+ln^2x)d(lnx)令lnx=u上式化为∫(1+u^2)du=u+u^3/3+c=lnx+(lnx)^3/3+c

1/x(x+1)=1/x-1/(x+1)所以原式=∫[(ln(x+1)-lnx]*[1/x-1/(x+1)]dx=∫[(ln(x+1)-lnx]d[lnx-(ln(x+1)]=-∫[lnx-ln(x+

其实1/[x(x+1)]=(1/x)-1/(1+x)只不过是换了一种表达方式和位置而已

∫ln(x+1)dx=∫ln(x+1)d(x+1)=(ln(x+1))(x+1)-∫(x+1)d(ln(x+1))=(x+1)ln(x+1)-∫((x+1)/(x+1))dx=(x+1)ln(x+1)

再问：+c再答：对

∫ ln(x^2 -1)dx 步骤

ln(x^2-1)=ln(x+1)+ln(x-1)∫ln(x^2-1)dx=∫ln(x+1)d(x+1)+∫ln(x-1)d(x-1)分部积分：原式=(x+1)ln(x+1)-∫(x+1)d(ln(x

∫ln(1+√x)dx

分部积分法.I=∫ln(1+√x)dx=xln(1+√x)-(1/2)∫√x/(1+√x)dx=xln(1+√x)-∫x/(1+√x)d√x令t=√x,则I1=∫x/(1+√x)d√x=∫t^2dt/

∫1+x^2ln^2x/xlnxdx=∫1/xlnxdx+∫xlnxdx分开积分就行了.