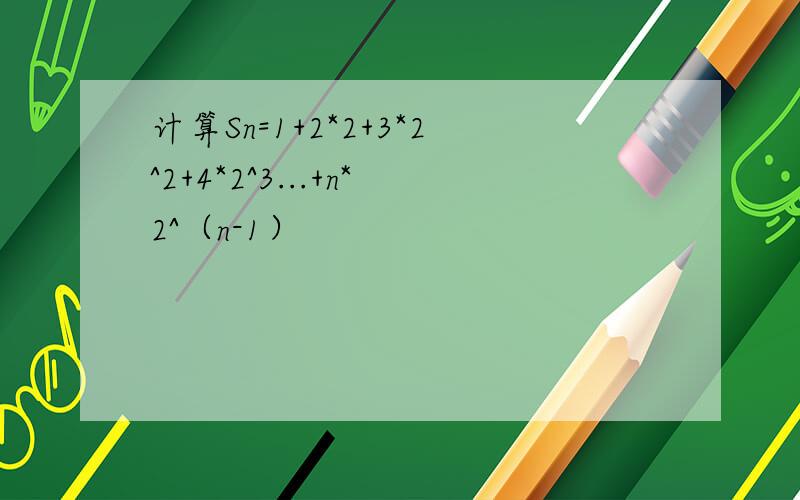计算Sn=1+2*2+3*2^2+4*2^3...+n*2^（n-1）

Sn=n(n+2)(n+4)的分项等于1/6[n(n+2)(n+4)(n+5)-(n-1)n(n+2)(n+4)]吗? 已知等差数列{an}的前n项和为Sn,且(2n-1)Sn+1 -(2n+1)Sn=4n²-1(n∈N*) Sn=3+2^n Sn-1=3+2^(n-1).则Sn-Sn-1=? 1+2+3+4+.+n,求Sn 数列Sn=(3n+1)/2-(n/2)an 已知数列{an}的首项是a1=1，前n项和为Sn，且Sn+1=2Sn+3n+1（n∈N*）． 已知数列{an}的前n项和为Sn=1+2+3+4+…+n,求f(n)= Sn /(n+32)Sn+1的最大值 已知Sn=2+5n+8n^2+…+(3n-1)n^n-1(n∈N*)求Sn 已知an=(2n+1)*3^n,求Sn an=（2^n-1）n,求Sn 数列求和：Sn=1/1*2*3+1/2*3*4+.+1/n*(n+1)*(n+2) 求Sn 求和：Sn=1*n+2*(n-1)+3*(n-2)+……+n*1