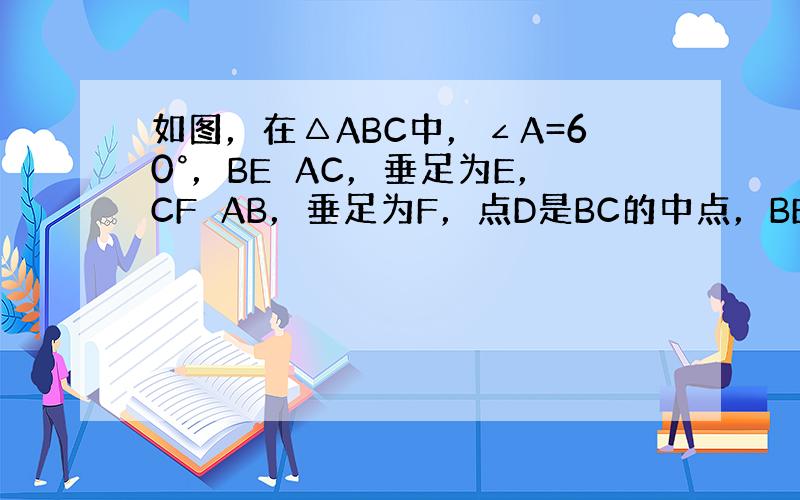
如图，在△ABC中，∠A=60°，BE⊥AC，垂足为E，CF⊥AB，垂足为F，点D是BC的中点，BE，CF交于点M．

如图,已知,在△ABC中,∠A=60°,AB=AC,BE⊥AC于E,CF⊥AB于F,点D为BC的中点,BE,CF交于点M 如图,已知BE⊥AC,垂足为E,CF⊥AB,垂足为F,BE与CF交于点D,且BD=CD求证：点D在∠A的平分线上.证AE 已知,在三角形ABC中,角A=60度,AB=AC,BE垂直于AC于E,CF垂直于AB于F,点D为BC的中点,BE、CF交 如图,已知,在三角形ABC中,角A=60,AB=AC,BE垂直于AC,CF垂直于AB,点D为BC中点,BE,CF交于点M 如图，在△ABC中，D为BC的中点，DE⊥DF交AB、AC于E、F，求证：BE+CF＞EF． 如图,在△ABC中,点D为BC的中点,点E为AB上一点,DF⊥DE交AC于F,求证：BE+CF＞EF △ABC在中∠A=90°,AB=AC,M是AC边的中点,AD⊥BM交BC于D,交BM于E,CF//AB交AD延长线与点F 如图,在△abc中,∠abc=45°,cd⊥ab,be⊥ac,垂足分别为点d,e,f为bc的中点,be与df、dc分别交 如图,在△ABC中,D是BC的中点,DE⊥AB于E,DF⊥AC于点F,BE=CF．AD平分∠BAC.求证：AD平分∠ED 如图,在三角形ABC中,D是BC的中点,DE垂直于AB,DF垂直于AC,垂足分别是E,F,BE=CF. 如图，在△ABC中，D是BC的中点，DE⊥AB于E，DF⊥AC于点F，且BE=CF，求证：AD⊥BC． 如图,三角形ABC中,∠B+∠C=2∠A,BE⊥AC,CF⊥AB,垂足分别为E、F,又D是BC 的中点,试判断△DEF