5.lim(e^x^2) －1/arctan x-0

来源：学生作业帮编辑：大师作文网作业帮分类：数学作业时间：2024/11/06 19:21:51

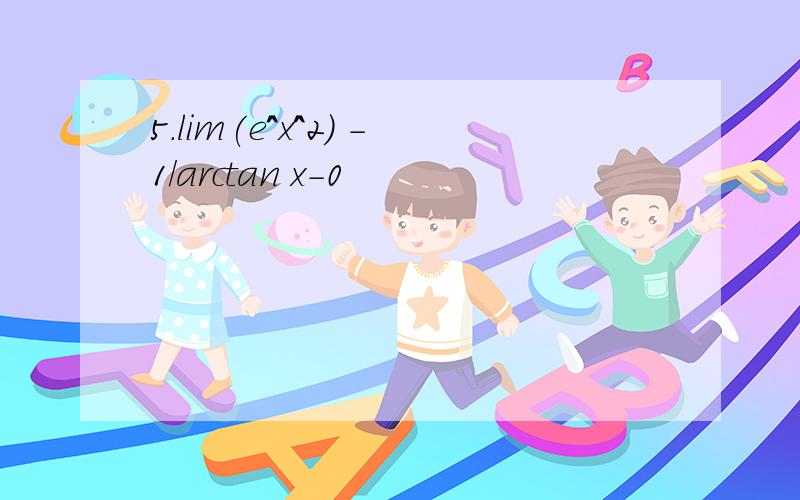
我猜了一下是不是下面这个极限：
exp(x^2) - 1
lim --------------------------------------------
x→0 arctan[sqrt(1 + x + x^2 ) - 1]
由于在 x→0 的时候分子分母都趋近于0,所以用洛比达法则
exp(x^2)*2x
= lim --------------------------------------------
x→0 1 1/2*（2x+1）
--------------------------------- * -------------------
2*sqrt(1 + x + x^2 ) - x + x^2 sqrt(1 + x + x^2 )
0
= ----------
1/2 * 1/2
= 0
或者你的意思是下面这个极限：
exp(x)^2 - 1
lim --------------------------------------------
x→0 arctan[sqrt(1 + x + x^2 ) - 1]
由于在 x→0 的时候分子分母都趋近于0,所以用洛比达法则
2*exp(x)*exp(x)
= lim --------------------------------------------
x→0 1 1/2*（2x+1）
--------------------------------- * -------------------
2*sqrt(1 + x + x^2 ) - x + x^2 sqrt(1 + x + x^2 )
2*1*1
= ----------
1/2 * 1/2
= 8
GOOD LUCK~

求lim e^(1/x^2)*arctan((x^2+2-1)/(x+1)*(x-2)) 当x趋近于0,-1,2的值求极限：lim 2(x+1)arctan(1/x) (x趋于0 ) 求极限lim(x趋于0)[arcsin(2x)/arctan(3x)] 求极限lim(x~0)((e^x+e^2x+e^3x)/3)^1/x lim(x->0)ln(1+2x)/e^x-1 lim[(1-e^(-x))^1/2]/x x趋于0 lim(x→0)(1-x^2-e^-x)/sinx lim sin 2x / sin 5x lim arctan x / x lim(x->0+) e^(1/x) lim(x+e^2x)^(1/sinx) 求这个的极限lim(x→无穷)arctan(x^2+x+1/x^2+x-2)的一些问题当x趋近0时 lim [e^x-e^(-x)]/x(1+x^2)