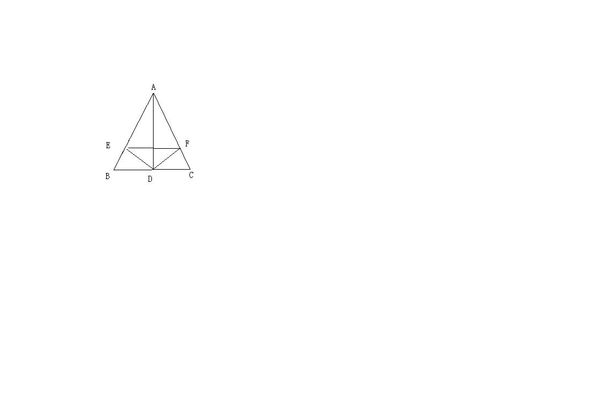
证等腰三角形的证明题如果,已知在△ABC中,AD是角平分线,DE⊥AB,DF⊥AC,E.F分别为垂足,求证：AD⊥EF

证等腰三角形的证明题如果,已知在△ABC中,AD是角平分线,DE⊥AB,DF⊥AC,E.F分别为垂足,求证：AD⊥EF 已知:如图,AD是△ABc的角平分线,DE⊥AB,DF⊥Ac,垂足分别为E、F.求证:AD垂直平分EF. 已知AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E、F.求证:AD垂直平分EF 如图,已知:在△ABC中,∠BAC的角平分线交BC于D,且DE⊥AB,DF⊥AC,垂足分别是E,F求证:AD是EF的垂直 AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为E、F,连接EF,EF与AD交于G,AD与EG垂直吗?证明你 AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F,连接EF,EF与AD相交于点G.求证：AD是EF的垂 如图,AD是△ABC的角平分线,BE⊥AB,DF⊥AC,垂足分别为E、F.求证：AD垂直平分EF 如图,已知:在△ABC中,∠BAC的平分线交BC于D,且DE⊥AB,DF⊥AC,垂足分别是E、F.求证：AD是EF的垂直 已知,如图,△ABC中AD是∠A的平分线,DE⊥AB,DF⊥AC,垂足分别为E,F,求证：（1）AE=AF （2）EF⊥ 如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为E.F连接EF,EF与AD交于G,AD与EF垂直吗?证 已知:如图,AD是△ABC的角平分线,DE⊥AB、DF⊥AC,点E、F为垂足,连接E、F.求证：AD垂直平分EF 如图,在△ABC中,AD是∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,求证：AD⊥EF.