已知等差数列an中,公差d>0,首项a1>0,bn=1/anan+1,数列bn的前n项和为Sn,则limSn=

来源：学生作业帮编辑：大师作文网作业帮分类：数学作业时间：2024/11/11 05:33:50

根据bn=1/(an*a(n+1)),我们知道,bn=[1/an-1/a(n+1)]/d.
因此,Sn=[1/a1 - 1/a2 + 1/a2 - 1/a3 +...+ 1/a(n-1) - 1/an]/d=[1/a1 - 1/an]/d.
我们又知道,a1>0,d>0,所以,lim an = ∞,因此,lim Sn=1/(a1*d).

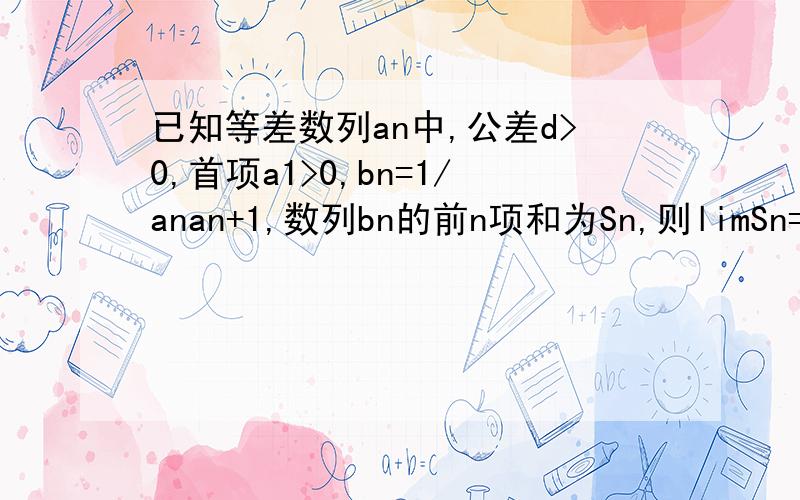
已知等差数列an中,公差d>0,首项a1>0,bn=1/anan+1,数列bn的前n项和为Sn,则limSn= 已知数列{an}是等差数列,公差d>0,前n项和Sn=【(an+1)/2】^2,bn=(-1)^n*Sn,求数列{bn} 已知数列{an}的前n项和为Sn，a1=3且an+1=2Sn+3，数列{bn}为等差数列，且公差d＞0，b1+b2+b3 已知{an}是公差为d的等差数列，它的前n项和为Sn，S4=2S2+4，bn＝1+anan．已知等差数列{an}的首项a1=1,公差d=1,前n项和为Sn,bn=1/Sn 求证:b1+b2+.+bn 设数列an前n项和Sn已知a1=a2=1 bn=nSn+（n+2）an数列bn公差为d的等差数列n属于N... 已知数列{An}的前n项和为Sn,A1=A2=1,bn=nSn+（n+2)An,数列{bn}是公差为d的等差数列, 已知数列｛an｝是公差为d的等差数列,d≠0且a1=0,bn=2^(an)(n属于N*）,Sn是｛bn｝的前n项和,Tn 已知{an}是公差为d的等差数列,bn=1/n(a1+a2+……an),数列{an}、{bn}的前n项和分别是Sn、Tn 若Sn是公差不为0的等差数列{an}的前n项和,且S1,S2,S4成等比数列设bn=3/anan+1,Tn是数列{bn 已知等差数列（an）的首项a1=1,公差d=1,前n项和为Sn,bn=1/Sn,求数列（bn）的通项公式在公差d≠0的等差数列{an}和等比数列{bn}中,已知a1=1,a1=b1,a8=b3,求{an+bn}的前n项和sn