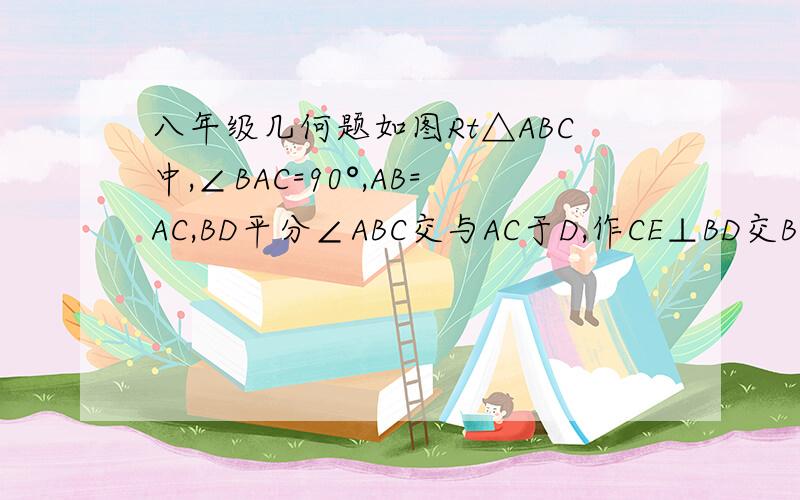八年级几何题如图Rt△ABC中,∠BAC=90°,AB=AC,BD平分∠ABC交与AC于D,作CE⊥BD交BD的延长线于

八年级几何题如图Rt△ABC中,∠BAC=90°,AB=AC,BD平分∠ABC交与AC于D,作CE⊥BD交BD的延长线于 Rt△ABC中,∠BAC=90°,AB=AC,BD平分∠ABC交与AC于D,作CE⊥BD交BD的延长线于E,交BA的延延 如图，Rt△ABC中，∠BAC=90°，AB=AC，BD平分∠ABC交AC于D，作CE⊥BD交BD的延长线于E，过A作A 1.如图,在Rt△ABC中,∠BAC=90°AB=AC,BD平分∠ABC,与AC交于点D,CE⊥BD交BD的延长线与点E 如图,在Rt△ABC中,AB=AC,∠BAC=90°,BD平分∠ABC交AC于点D,CE⊥BD交BD的延长线于点E. 如图,在Rt△ABC中,∠BAC=90°,AB=AC,BD平分∠ABC,CE⊥BD交BD的延长线于E,BA,CE的延长线 已知：如图,在等腰三角形ABC中,∠BAC=90°,BD平分∠ABC,交AC于点D,过点C作CE⊥BD,交BD的延长线于 如图所示,在△ABC中,AB=AC,∠A=90°,BD平分∠ABC交AC于D,CE⊥BD交BD的延长线于点E,则CE=_ 已知:如图在△ABC中,∠BAC=90°,AB=AC,BD平分∠ABC,CE⊥BD交BD的延长线于E.求证BD=2CE. Rt⊿ABC中,AB=AC,∠BAC=90,BC平分∠ABC,过点C作CE⊥BD交BC延长线于点E,求证：BD=2CE. 三角形数学练习题如图,已知:在△ABC中,∠BAC=90°,AB=AC,BD平分∠ABC交AC于D,且CE⊥BD延长线于 初三数学几何题 在Rt三角形ABC中,AB=AC ∠BAC=90° 过点C作CE垂直BD 交BD延长线于点E 求证 BD