已知RT三角形ABC中,ACB=90,将RT三角形ABC绕点C顺时针旋转90,得到三角形DHC,DH的延长线交AB于点G

来源：学生作业帮编辑：大师作文网作业帮分类：数学作业时间：2024/11/11 11:17:41

已知RT三角形ABC中,ACB=90,将RT三角形ABC绕点C顺时针旋转90,得到三角形DHC,DH的延长线交AB于点G,连接AD,作DE平行AB,BE平行AD,交于点E,点P是线段DE上的动点,连接AP,PB,AP交DG于点F,连接BF,AG=2,BG=3.
1,求DH的长
2,设FG=x,AP=y,求y与x的函数关系式（不要求写自变量取值范围）
3,是否存在点P,使得APB=ABF,若存在,求出FG的长,若不存在,请说明理由.

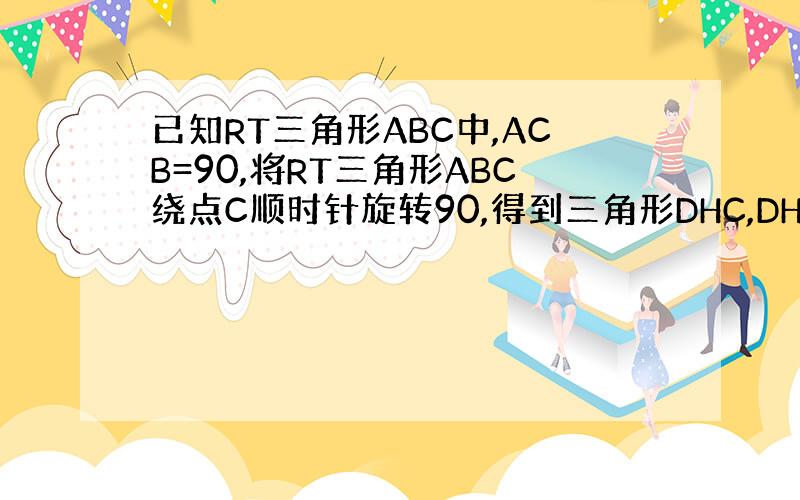
1,DH=AB=AG+BG=2+3=5
2,设FG=x,AP=y,求y与x的函数关系式（不要求写自变量取值范围）
将RT三角形ABC绕点C顺时针旋转90,故DH⊥AB、△AGH∽△DGB.
AG/DG=GH/GB,即：2/(5+GH)=GH/3,GH=1,
DG=DH+GH=6.
作PG'垂直于AB,则：PG'=DG=5+1=6 ,△AFG∽△APG' 、 AF=√（4+x²）
得：AF/AP=FG/PG' 有：√（4+x²）/y=x/6 y=6√(X²+4) /X
整理得：36x²-x²y²+144=0
3,是否存在点P,使得APB=ABF,若存在,求出FG的长,若不存在,请说明理由.
若存在∠APB=∠ABF 又∠BAP=∠FAB.则：△BAF∽△PAB 有：AB/AP=AF/AB.
即：5/y=√(X²+4) /5 y√(x²+4)=25,6(X²+4)/X=25,X=3/2或8/3.
AD∥BE,DE∥AB,故四边形ABED为平行四边形,DE=AB=5.
X=8/3时,GF/DF=AG/PD,即(8/3)/(6-8/3)=2/PD,PD=2.5＜5
X=3/2时,GF/DF=AG/PD,即(3/2)/(6-3/2)=2/PD,PD=6＞5不合题意,舍去.
故：存在点P,使得∠APB=∠ABF,此时FG的长为8/3.

已知RT三角形ABC中,ACB=90,将RT三角形ABC绕点C顺时针旋转90,得到三角形DHC,DH的延长线交AB于点G RT三角形ABC'是由RT三角形ABC绕点A顺时针旋转得到的,连接CC'交斜边AB于点E,CC'的延长线交BB'于点F 如图,在RT三角形ABC中,∠C=90°,M为AB边上中点,将RT三角形ABC绕点M旋转,使点C与点A重合得到三角形DE 已知如图在rt三角形ABC,角ACB=90度,将三角形ABC绕点C按顺时针方向旋转得三角形A1B1C,CB1,A1B1, 在Rt三角形ABC中,角ACB=90度,点o在AC上,圆O过点A交AB于D,与AC的延长线交于G,DB的中垂线EF交CB 在RT三角形ABC中,角ACB=90度,AB=10,BC=6,将△abc绕点c顺时针旋转90°到△a'b'c,m是a'b 在Rt三角形ABC中,角ACB=90度,BC=3,AC=4,AB的垂直平分线DE交BC的延长线于点E,则如图,在Rt三角形ABC中,𠃋ACB＝90度,AB的垂直平分线DE交AC于点E,交BC的延长线于F,若& 将Rt三角形ABC绕点c顺时针旋转90度到三角形A’B’C’位置如图,已知在rt三角形abc中,角acb=90度,cd垂直于ab于d,e是ac中点,de的延长线与bc的延长线交于点f 在Rt三角形abc中,角acb=90,边ac的垂直平分线ef交ac于点e,交ab于点f,bg垂直ab,交ef的延长线于点如图,已知在三角形ABC中,AB=AC,若将三角形ABC绕点C顺时针旋转180°得到三角形FEC