∫x²√1-x²dx
来源:学生作业帮助网 编辑:作业帮 时间:2024/11/17 02:12:41
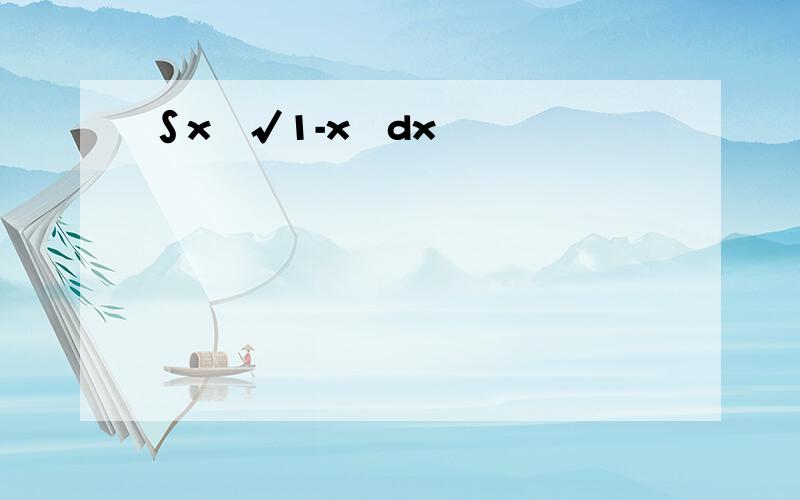
∫(3x+1)/√(4+x²)dx令x=2tanθ,dx=2sec²θdθ=∫(6tanθ+1)/(2secθ)•(2sec²θ)dθ=∫(6secθtanθ
∫f(x)dx=xf(x)-∫xdf(x)∫f(x)dx=xf(x)-∫xdx/√(1+x^2)df(x)=dx/√(1+x^2)f(x)=∫dx/√(1+x^2)=ln|x+√(1+x^2)|+Cx
1/4*Ln(2x+1)+1/(4(2x+1))√(x²+4)再问:没看懂上面是两道题再答:知道啊,不是有两答案嘛就是换元法,两个属于同一类。将分母中的1+2x和x²+4换元,再进
这个是考你的换元能力来的,~~~~不明白的就追问吧~~~~希望楼主采纳!O(∩_∩)O谢谢
∫arctan(1+√x)dx换元t=arctan(1+√x),(tant-1)^2=x=∫td(tant-1)^2=t(tant-1)^2-∫(tant-1)^2dt=t(tant-1)^2-∫(s
∫√(1+x)dx=∫(1+x)^1/2dx=2/3(1+x)^3/2再问:∫√(1+x^2)dx打小个平方不好意思再答:∫√(1+x^2)dx=x√(1+x^2)-∫x*x*√(1+x^2)dx=x
∫inx/√xdx=2∫inxd√x=2√xlnx-2∫√x*1/xdx=2√xlnx-2∫1/√xdx=2√xlnx-4√x+c
令√(1+e^x)=u,则e^x=u^2-1,x=ln(u^2-1),dx=2udu/(u^2-1)I=∫√(1+e^x)dx=∫2u^2du/(u^2-1)=2∫[1+1/(u^2-1)]du=2u
令x+1=3tanθ,则dx=3sec²θdθ∫1/√[(x+1)²+9]dx=∫1/√(9tan²θ+9)•(3sec²θdθ)=∫1/(3sec
x=sinadx=cosada√(1-x²)=cosa∴原式=∫cos²ada=1/2∫(cos2a+1)da=1/4·sin2a+1/2a+c=1/2x√(1-x²)+
令x=tant则dx=sec^2tdt于是∫dx/[x(x^2+1)]=∫sec^2t/[tantsec^2t]dt=∫dt/tant=∫(cost/sint)dt=∫(1/sint)dsint=ln
Log就是ln的意思.后面自己加一个常数C即可.再答:有什么不懂得尽管问再问:但我再求导你的结果检验得不到题目的式子啊?再答:不可能吧,你合并没?我这是用MATLAB计算得到的结果,手算过程技巧就是换
一步一步微分、积分并用,就可以还原出原函数,也就是一些教师所说的“还原法”,或“凑微分法”:∫(arctan√x)/[√x×(1+x)]dx=2∫(arctan√x)/[1+x]d√x=2∫(arct
∫dx/[x√(1-x^4)]letx^2=siny2xdx=cosydy∫dx/[x√(1-x^4)]=(1/2)∫(1/siny)dy=(1/2)ln|cscy-coty|+C=(1/2)ln|1
∫dx/√[1-e^(-2x)]lete^(-x)=siny-e^(-x)dx=cosydy∫dx/√[1-e^(-2x)]=∫-cscydy=-ln|cscy-coty|+C=-ln|e^x-(e^
分部积分法.I=∫ln(1+√x)dx=xln(1+√x)-(1/2)∫√x/(1+√x)dx=xln(1+√x)-∫x/(1+√x)d√x令t=√x,则I1=∫x/(1+√x)d√x=∫t^2dt/