如图,PA垂直于矩形ABCD所在平面,M,N分别为AB,PC的中点,若∠PDA=45°,求证：MN垂直于平面PCD

来源：学生作业帮编辑：大师作文网作业帮分类：数学作业时间：2024/11/10 11:01:05

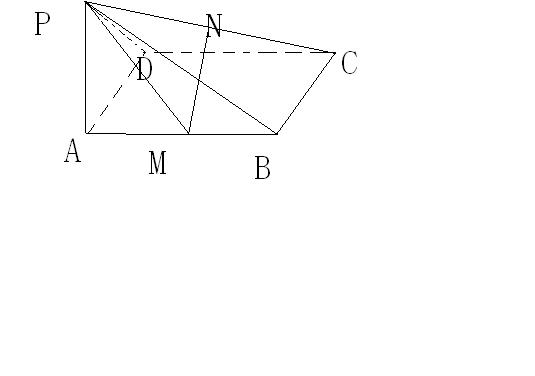
证明：取PD中点E,连接EN、AE
因为 E为PD中点,N为PC中点
所以 EN//且=1/2CD
在矩形ABCD中
所以 AB//且=AB
因为 M为AB中点
所以 EN//且=AM
所以四边形AENM为平行四边形,MN//AE
在Rt三角形ADP中
因为 ∠PDA=45°,AE为PD中线
所以 AE垂直于PD
则 MN垂直于PD
因为 PA垂直于矩形ABCD所在平面
所以 CD垂直于AD,CD垂直于PA
因为 AD、PA交于A
所以 CD垂直于面ADP
则 CD垂直于AE
因为 AE垂直于PD,CD、PD交于D
所以 AE垂直于面PCD
即 MN垂直于面PCD

如图,PA垂直于矩形ABCD所在平面,M,N分别为AB,PC的中点,若∠PDA=45°,求证：MN垂直于平面PCD 已知PA垂直于矩形ABCD所在平面,M,N分别是AB,PC的中点,若∠PDA=45度,求证MN垂直平面PCD. 已知PA垂直于矩形ABCD所在的平面,M、N分别是AB、PC的中点,若＜PDA=45°,求证：MN⊥平面PCD 已知PA垂直于矩形ABCD所在的平面,M,N分别是AB,PC的中点,角PDA为45度,求证：MN垂直面PCD 如图,PA⊥矩形ABCD所在的平面,M,N分别是AB,PC的中点,∠PDA=45°,求证;MN⊥平面PCD PA垂直于矩形ABCD所在平面,PA=PD,点M,N分别是AB,PC的中点.求证:MN⊥平面PCD 如图,已知PA垂直于矩形ABCD所在的平面,M,N分别是AB,PC的中点,求证：MN垂直于CD. 已知PA垂直矩形ABCD所在平面,M,N分别是AB,PC的终点.（1）求证：MN垂直CD；(2)若角PDA=45°,求证 PA垂直于底面ABCD,四边形ABCD是矩形,PA=AD,M、N分别是AB、PC的中点,求证平面DMN垂直于平面PCD? 如图,PA垂直于矩形ABCD所在平面,M,N分别是AB,PC中点,求证 MN∥平面PAD ABCD为矩形,向量PA垂直平面ABCD,PA=AD,M,N分别为PC,AB中点,求证MN垂直平面PCD ABCD为矩形,PA垂直平面ABCD,PA=AD,M,N分别为PC,AB中点,求证：MN垂直平面PCD