gcd(ac,bc) = c* gcd(a,b)
来源:学生作业帮 编辑:大师作文网作业帮 分类:数学作业 时间:2024/11/11 08:19:42
gcd(ac,bc) = c* gcd(a,b)
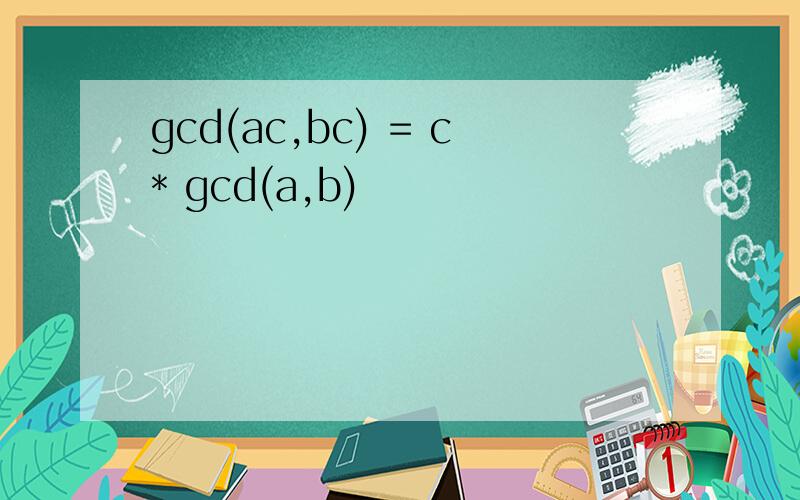
gcd表示最大公约数
1) 首先证明c*gcd(a,b)是ac、bc的一个公约数
因为c | c,gcd(a,b) | a,所以c*gcd(a,b) | ac
因为c | c,gcd(a,b) | b,所以c*gcd(a,b) | bc
于是c*gcd(a,b)是ac、bc的一个公约数
2) 其次证明c*gcd(a,b)是ac、bc的最大公约数
最大公约数的性质是,两个数的最大公约数可以整除这两个数的其他公约数
于是c*gcd(a,b) | gcd(ac,bc),假设gcd(ac,bc)=k*c*gcd(a,b),k>=1
因为k*c*gcd(a,b) | ac,所以k*gcd(a,b) | a
因为k*c*gcd(a,b) | bc,所以k*gcd(a,b) | b
于是k*gcd(a,b)是a、b的一个公约数,根据最大公约的性质,k*gcd(a,b) | gcd(a,b),于是k=1
从而gcd(ac,bc)=c*gcd(a,b)
1) 首先证明c*gcd(a,b)是ac、bc的一个公约数
因为c | c,gcd(a,b) | a,所以c*gcd(a,b) | ac
因为c | c,gcd(a,b) | b,所以c*gcd(a,b) | bc
于是c*gcd(a,b)是ac、bc的一个公约数
2) 其次证明c*gcd(a,b)是ac、bc的最大公约数
最大公约数的性质是,两个数的最大公约数可以整除这两个数的其他公约数
于是c*gcd(a,b) | gcd(ac,bc),假设gcd(ac,bc)=k*c*gcd(a,b),k>=1
因为k*c*gcd(a,b) | ac,所以k*gcd(a,b) | a
因为k*c*gcd(a,b) | bc,所以k*gcd(a,b) | b
于是k*gcd(a,b)是a、b的一个公约数,根据最大公约的性质,k*gcd(a,b) | gcd(a,b),于是k=1
从而gcd(ac,bc)=c*gcd(a,b)
gcd(ac,bc) = c* gcd(a,b)
如果gcd(a b)=1 ,证明gcd(ab,c)=gcd(a,c)*gcd(b,c) 怎么证阿
如何证明gcd(a,b,c)=gcd(gcd(a,b),c)
证明:gdc(a,bc)整除(gcd(a,b)*gcd(a,c))
gcd(a,b) = gcd (a+b,lcm (a,b))
如何证明gcd(a,b)=gcd(a,a+b)
b==0?a:gcd(b,
1.编写最大公约数的递归函数gcd():若a=b,gcd(a,b)=a;若a>b,gcd=(a-b,b);若ab,gcd
如何证明gcd(a,b) = gcd(a+b,lcm(a,b))
gcd(a,
如何证明 gcd(a,b) = gcd( a+b,lcm (amb))
C语言简单计算!a=5,b=10,c=15g=gcd(a,b)printa("%d",gcd(g,c))请问这里g=gc