数列{an}的前n项和Sn=k·(2^n)+m,k≠0且a1=3

来源：学生作业帮编辑：大师作文网作业帮分类：数学作业时间：2024/11/17 19:56:30

数列{an}的前n项和Sn=k·(2^n)+m,k≠0且a1=3
(1)求数列{an}的通项公式
(2)设bn=n/(an),Tn是数列{an}的前n项和,求使得Tn

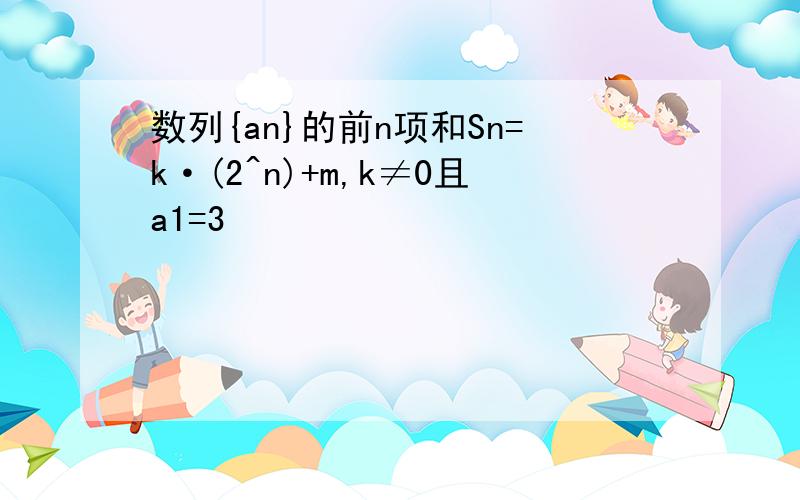
$数列{an}的前n项和Sn=k·(2^n)+m,k≠0且a1=3$

（1）an=Sn-Sn-1=k（2^n-2^n-1）=k2^n-1
a1=3代入上式得k=3
所以an=3*2^n-1
(2) bn=n/an=n/(3*2^n-1)
Tn=1/3+2/6+3/12+…+bn
1/2（Tn）=1/6+2/12+3/24+…+1/2（bn）
相减可得1/2（Tn）=1/3+1/6+1/12+…+1/（3*2^n）-1/2（bn）=2/3（1-（1/2）^n）-n/（3*2^n）
化简得Tn=（4*2^n-4-n）/（3*2^n）
由极限知识得Tn极限值=4/3
所以Tn小于4/3 解得m（min）=40
符号不好打,希望你看得懂.

数列{an}的前n项和Sn=k·(2^n)+m,k≠0且a1=3 等差数列｛an｝的首项a1>0,前n项和为sn,且sm=sn(m,k为常数且m≠k),则①s(m+k)=?②当n为何值：设Sn为数列{an}的前n项和（n=1,2,3…）.按如下公式定义数列{an}:a1=m(m∈N*),对任意k∈N*,k 等差数列{An}中,首项a1>0,前n项和为Sn,且Sm=Sk(m≠k)当n为和值时,Sn取最大值? 数列{an}的前n项和为Sn,若a1=1,Sn大于0,且an=2Sn平方除以(2Sn-1),设存在正整数k, 已知数列{an}的前n项和Sn=-1/2n^2+kn,k∈N*,且Sn的最大值为8.1）确定常数k, 已知数列{an}的前n项和Sn=-1/2n^2+kn,k∈N*,且Sn的最大值为8.1）确定常数k 已知数列{an}满足ak+a(n-k)=2,(k,n-k∈N*),则数列{an}的前n项和Sn= 已知数列｛An}的前n项和Sn满足S(n+1)=KSn+2(n属于N*)且a1=2,a2=1 (1) 求K的值和Sn的表已知数列an的前n项和为Sn,且满足an+2Sn·S(n-1)=0(n≥2),a1=1.5 已知数列{an}a1=2前n项和为Sn 且满足Sn Sn-1=3an 求数列{an}的通项公式an 已知数列{an}的首项是a1=1，前n项和为Sn，且Sn+1=2Sn+3n+1（n∈N*）．