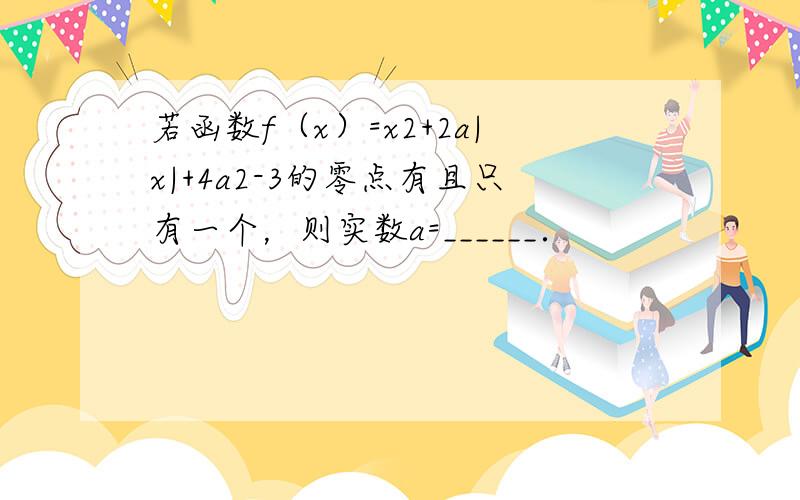
若函数f(x)=x2+2a|x|+4a2-3的零点有且只有一个,则实数a=______.
若函数f(x)=x2•lna-2x+2在区间(1,2)内有且只有一个零点,那么实数a的取值范围是______.
已知函数f(x)=x2+(a2-1)x+(a-2)的一个零点比1大,一个零点比1小,则实数a的取值范围______.
已知函数f(x)=4x+m•2x+1有且只有一个零点,则实数m的值为______.
若函数f(x)=|x2-4x|-a有三个零点,则实数a的值是______.
若函数f(x)=mx2-2x+3只有一个零点,则实数m的取值是______.
已知f(x)=a-x2-4x(x<0)f(x-2)(x≥0),且函数y=f(x)-2x恰有3个不同的零点,则实数a&nb
函数f(x)=|x2-2x|-a有四个零点,则实数a的取值范围是 ______.
若函数f(x)=x2+2x+a没有零点,则实数a的取值范围是______.
已知函数f(x)=3x2+4x-a,若函数f(x)在区间(-1,1)内存在零点,则实数a的取值范围为______.
已知函数f(x)=x2+ax-4在区间(0,1)内只有一个零点,则a的取值范围是______.
已知函数f(x)=x^2-2ax+1,求在【1,3】内有且只有一个零点时,实数a的取值范围.
已知函数f(x)=x2+(a2-1)x+(a-2)的一个零点比1大,一个零点比1小,则实数a的取值范围