一道初二四边形练习、 2.如图,△ABC中,AB=AC,E是AB上一点,以点E为圆心,EB为半径画弧交BC于点D,连结E
来源:学生作业帮 编辑:大师作文网作业帮 分类:综合作业 时间:2024/11/11 17:19:25
一道初二四边形练习、
2.如图,△ABC中,AB=AC,E是AB上一点,以点E为圆心,EB为半径画弧交BC于点D,连结ED,并延长ED到F,使EF=AB,连结FC,问∠F和∠A是否相等?为什么?
将理由写出来

2.如图,△ABC中,AB=AC,E是AB上一点,以点E为圆心,EB为半径画弧交BC于点D,连结ED,并延长ED到F,使EF=AB,连结FC,问∠F和∠A是否相等?为什么?
将理由写出来

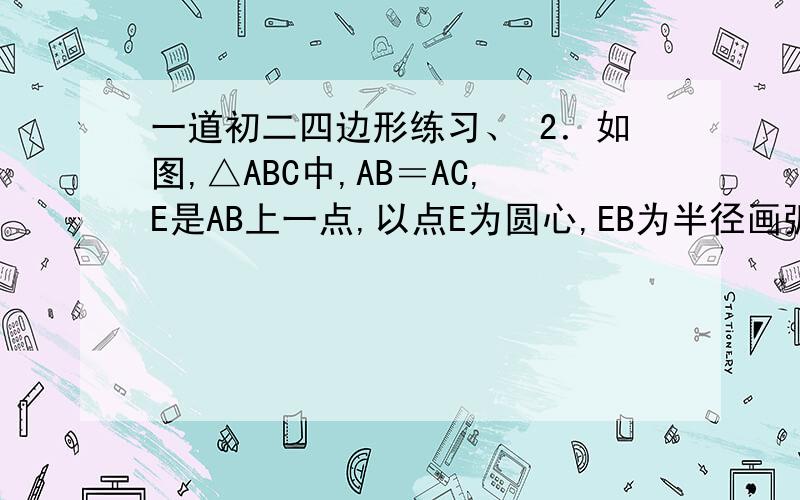
答:∠F=∠A
证明:∵以点E为圆心,EB为半径画弧交BC于点D
∴BE=DE(同圆的半径相等)
∴∠EBD=∠EDB(等边对等角)
又∵AB=AC
∴∠EBD=∠ACB(等边对等角)
∴∠EDB=∠ACB(等量代换)
∴AC‖EF(同位角相等,两直线平行)
又∵AB=AC,EF=AB
∴AC=EF(等量代换)
∴四边形AEFC是平行四边形
∴∠F=∠A(平行四边形的对角相等)
证明:∵以点E为圆心,EB为半径画弧交BC于点D
∴BE=DE(同圆的半径相等)
∴∠EBD=∠EDB(等边对等角)
又∵AB=AC
∴∠EBD=∠ACB(等边对等角)
∴∠EDB=∠ACB(等量代换)
∴AC‖EF(同位角相等,两直线平行)
又∵AB=AC,EF=AB
∴AC=EF(等量代换)
∴四边形AEFC是平行四边形
∴∠F=∠A(平行四边形的对角相等)
一道初二四边形练习、 2.如图,△ABC中,AB=AC,E是AB上一点,以点E为圆心,EB为半径画弧交BC于点D,连结E
在△ABC中,AB=AC,O是AB上一点,以O为圆心的圆经过点A,交AB于点F,与BC相切于点E.点D为BC的中点,连结
如图,在△ABC中,∠C=90°,以AB上一点O为圆心,OA长为半径的圆与BC相切于点D,分别交AC、AB于点E、F.若
如图,在△ABC中,∠C=90°,以AB上一点O为圆心,OA长为半径的圆与BC相切于点D,分别交AC、AB于点E、F.
如图,在△ABC中,∠C= 90°,以AB上一点O为圆心,OA长为半径的圆与BC相切于点D,分别交AC、AB于点E、F.
△ABC中,AB=AC,E为AB上一点,以点E为圆心,EB为半径画弧
如图,在Rt△ABC中,∠ABC=90,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,且AD
如图,在△ABC中,∠C=90°,AC+BC=8,点O是斜边AB上一点,以O为圆心的⊙O分别与AC,BC相切于点D,E.
在三角形ABC中AB=AC,E是AB的中点,以E为圆心,EB为半径画弧,交BC于点D, 连接ED并延长到点F,使D
已知,如图,△ABC中,AB=AC,以点A为圆心,小于AB长(大于BC变上的高)为半径长作圆弧,交BC于D、E,求证:B
如图,在△ABC中,∠C=90°,AC+BC=8,点O是斜边AB上一点,以O为圆心的⊙O分别与AC、BC相切于点D、E
如图,Rt△ABC中,∠C=90°,以AB上点O为圆心,BO为半径的圆交AB的中点于E,交BC于D,且与AC切于点P