如下图为函数y=Asin(ωx+φ)+c(A<0,ω>0,φ>0)图像的一部分
来源:学生作业帮 编辑:大师作文网作业帮 分类:数学作业 时间:2024/11/12 04:30:44
如下图为函数y=Asin(ωx+φ)+c(A<0,ω>0,φ>0)图像的一部分
1)求此函数的周期及最大值和最小值 2)求与这个函数图象关于直线x=2对称的函数解析式
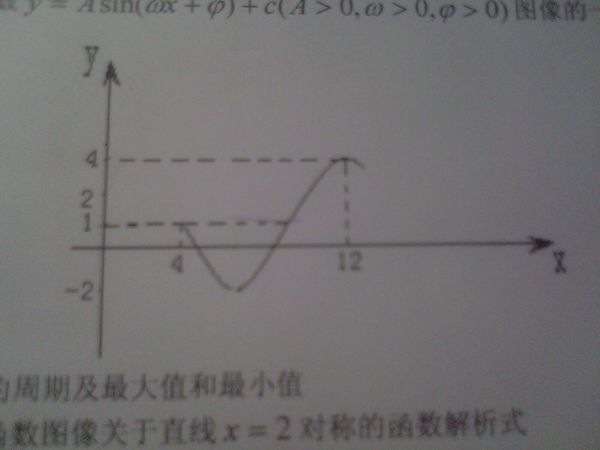
1)求此函数的周期及最大值和最小值 2)求与这个函数图象关于直线x=2对称的函数解析式


(1)由图形可知,从4~12的的图象是该函数的三分之二个周期的图象,
所以 A=1/2*(4+2)=3
c=12(4-2)=1,
所以 函数的最大值=4,最小值= -2
因为 2/3*2π/ω=8,
所以 ω=π/6,
故 T=12.
把x=12,y=4代入上式,得 ϕ=π/2
解析式为:y=3cosπx/6+1. [ sin(πx/6+π/2)=cosπx/6)]
(2)设所求(关于直线x=2对称的函数)的图象上任一点(x,y)关于直线x=2的对称点为(x1,y1),
则 x1=4-x,y1=y
代入 y=3cosπx/6+1
可得 y=3cos(2π/3-πx/6)+1
∴ 函数解析式为:y=3cos(2π/3-πx/6)+1
再问: 不好意思问一下,你做的和答案上一模一样,但是我的老师后来说,答案是错的,他说4~12应该是四分之三个周期,所以为什么你会得到三分之二个周期呢?
再答: 4~12的的图象是该函数的三分之二个周期的图象计算依据: (12-4)/12=8/12=2/3
所以 A=1/2*(4+2)=3
c=12(4-2)=1,
所以 函数的最大值=4,最小值= -2
因为 2/3*2π/ω=8,
所以 ω=π/6,
故 T=12.
把x=12,y=4代入上式,得 ϕ=π/2
解析式为:y=3cosπx/6+1. [ sin(πx/6+π/2)=cosπx/6)]
(2)设所求(关于直线x=2对称的函数)的图象上任一点(x,y)关于直线x=2的对称点为(x1,y1),
则 x1=4-x,y1=y
代入 y=3cosπx/6+1
可得 y=3cos(2π/3-πx/6)+1
∴ 函数解析式为:y=3cos(2π/3-πx/6)+1
再问: 不好意思问一下,你做的和答案上一模一样,但是我的老师后来说,答案是错的,他说4~12应该是四分之三个周期,所以为什么你会得到三分之二个周期呢?
再答: 4~12的的图象是该函数的三分之二个周期的图象计算依据: (12-4)/12=8/12=2/3
如下图为函数y=Asin(ωx+φ)+c(A<0,ω>0,φ>0)图像的一部分
如下图为函数y=Asin(wx+φ)(A>0,w>0,φ>0)图像的一部分
如下图为函数y=Asin(ωx+φ)+c,图像一部分,求这个函数关于x=2对称的解析式
如图为函数y=Asin(ωx+ϕ)+c(A>0,ω>0,ϕ>0)图象的一部分.
函数y=Asin(ωx+φ)的一个周期内的图像如下图,求Y的解析式.其中A>0,ω>0,-π
如图,已知正弦型函数y=Asin(wx+φ+)(A>0,m>0,++φ<π/2)的图像(的一部分),
已知函数y=asin(ωx+φ)+b的一部分图像如右图所示,如果A>0,ω>0,︱φ︳
已知函数y=asin(ωx+φ)+b的一部分图像如右图所示,如果A>0,ω>0,|φ|
函数y=Asin(ωx+φ)的图像如图所示,其中A>0,ω>0,0
如图为函数y=Asin(wx+a)+c图像的一部分,则函数解析式为
如图所示为函数y=Asin(wx+φ)+c(A>0,w>0,φ>0)图像的一部分(1求T及值max与min(2求此图象关
已知函数y=Asin(wx+φ)(A>0,w>0,|φ|>0)的一段图像如下图所示(1)求此函数解析式